Advertisements
Advertisements
Question
Isotherms of carbon dioxide gas are shown in figure. Mark a path for changing gas into liquid such that only one phase (i.e., either a gas or a liquid) exists at any time during the change. Explain how the temperature, volume and pressure should be changed to carry out the change.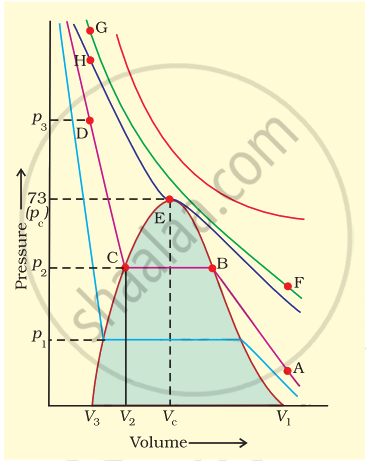
Solution
In isotherm of carbon dioxide, it is possible to change a gas into liquid or a liquid into gas by a process in which always a single phase is present.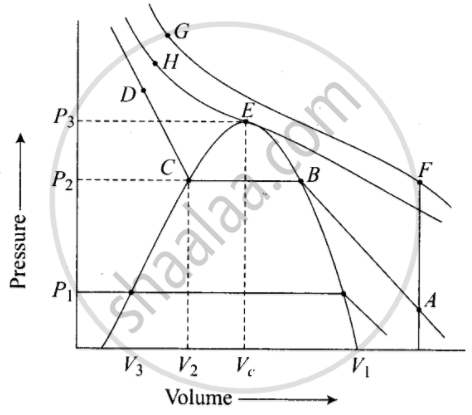
If we move vertically from point \[\ce{A}\] to \[\ce{F}\] by increasing the temperature, then we can reach the point G by compressing the gas at constant temperature along this (isotherm at 31.1°C). Now we can move vertically downwards to \[\ce{D}\] by lowering the temperature. As soon as we cross point \[\ce{H}\] on critical isotherm, we get liquid. If process is carried out at critical temperature, substance always remains in one phase. Hence the path for the change is \[\ce{A → F → G → H → D}\]
APPEARS IN
RELATED QUESTIONS
Calculate the volume occupied by 8.8 g of CO2 at 31.1°C and 1 bar pressure. R = 0.083 bar L K–1 mol–1.
Which of the following is the correct expression for the equation of state of van der Waals gas?
The value of the universal gas constant depends upon
Maximum deviation from ideal gas is expected from
Can a Van der Waals gas with a = 0 be liquefied? explain.
Suppose there is a tiny sticky area on the wall of a container of gas. Molecules hitting this area stick there permanently. Is the pressure greater or less than on the ordinary area of walls?
Explain whether a gas approaches ideal behavior or deviates from ideal behaviour if the temperature is raised while keeping the volume constant.
Explain whether a gas approaches ideal behavior or deviates from ideal behaviour if more gas is introduced into the same volume and at the same temperature.
Assertion (A): At constant temperature, pV vs V plot for real gases is not a straight line.
Reason (R): At high pressure all gases have \[\ce{Z}\] > 1 but at intermediate pressure most gases have \[\ce{Z}\] < 1.
In van der Waal's equation for the real gas, the expression for the net force of attraction amongst the gas molecules is given by:
