Advertisements
Advertisements
Question
किसी शांकवीय बर्तन के शीर्ष के एक छोटे छिद्र से, जिसका अक्ष ऊर्घ्वाधर है, पानी 1 cu cm/sec की दर से बह रहा है। बर्तन में पानी के सतह की तिर्यक ऊँचाई के घटने की दर उस समय ज्ञात कीजिए जब तिर्यक ऊँचाई 4 cm हैं। शांकवीय बर्तन का शीर्ष कोण `pi/6` है।
Solution
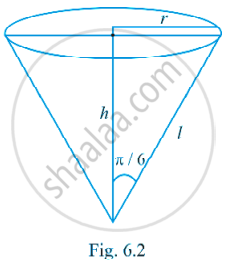
दिया हुआ है कि `"dv"/"dt"` = 1 cm3/s
जहाँ v शांकवीय बर्तन में पानी का आयतन है।
आकृति 6.2 से, l = 4 cm
h = `"l" cos pi/6`
= `sqrt(3)/2 "l"` तथा r = `"l" sin pi/6 = "l"/2`.
इसलिए, v = `1/3 pi"r"^2"h"`
= `pi/3 "l"^2/4 sqrt(3)/2 "l"`
= `(sqrt(3)pi)/24 "l"^3`
`"dv"/"dt" = (sqrt(3)pi)/8 "l"^2 "dl"/"dt"`
इसलिए, l = `(sqrt(3)pi)/8 16 * "dl"/"dt"`
⇒ `"dl"/"dt" = 1/(2sqrt(3)pi)` cm/s.
अतः, तिर्यक ऊँचाई के घटने की दर = `1/(2sqrt(3)pi)` cm/s
APPEARS IN
RELATED QUESTIONS
अवकलज का प्रयोग करके निम्नलिखित में से सन्निकट मान ज्ञात कीजिए।
(33)-1/5
`pi/4` अर्ध शीर्ष कोण वाले एक शांकवीय कीप (funnel) से, जिसकां शीर्ष नीचे की ओर है, कीप के पृष्ठ के क्षेत्रफल में 2cm2/sec की समान दर से उसके शीर्ष के एक छिद्र से पानी बह रहा है। पानी के सतह की तिर्यक ऊँचाई के घटने की दर उस समय ज्ञात कीजिए जब उसकी तिर्यंक ऊँचाई 4cm है।
सिद्ध कीजिए कि फलन f(x) = 4x3 – 18x2 + 27x – 7 का कोई उच्चिष्ठ अथवा निम्निष्ठ नहीं है।
अवकलों के प्रयोग द्वारा `sqrt(0.082)` का सन्निकट मान ज्ञात कीजिए।
वक्रों `x^2/"a"^2 - y^2/"b"^2` = 1 तथा xy = c2 के लम्बकोणीय प्रतिच्छेदन के लिए प्रतिबंध ज्ञात कीजिए।
फलन f(x) = `- 3/4 x^4 - 8x^3 - 45/2 x^2 + 105` के सभी स्थानीय उच्चिष्ठ तथा स्थानीय निम्निष्ठ बिंदुओं को ज्ञात कीजिए।
सिद्ध कीजिए कि `x + 1/x` का स्थानीय उच्चतम मीन उसके स्थानीय निम्नतम मान से कम है।
वक्र y2 = 4ax तथा x2 = 4by का प्रतिच्छेद कोण ज्ञात कीजिए।
उस महत्तम आयत का क्षेत्रफल ज्ञात कीजिए, जो दीर्घवृत्त `x^2/a^2 + y^2/b^2` = 1 के अंतर्गत स्थित है।
वक्र y2 = x पर वह बिंदु जहाँ स्पर्श रेखा x-अक्ष से `pi/4` कोण बनाती है।
यदि f (x) = sinx तो अंतराल `[(-pi)/2, pi/2]` में f का निम्निष्ठ मान ______ है।
नमक का एक गोलाकार गेंद पानी में इस प्रकार घुल रहा है कि किसी क्षण उसके आयतन के घटने की दर उसके पृष्ठीय क्षेत्रफल के समानुपाती है। सिद्ध कीजिए कि उसकी त्रिज्या एक अचर दर से घट रही है।
एक दूसरे से 45° पर झुकी हुई दो सड़कों के संधि-स्थल से दो मनुष्य A तथा B, एक ही समय v वेग से चलना प्रारम्भ करते हैं। यदि वे अलग-अलग सड़कों पर चलते हैं तो उनके परस्पर एक दूसरे से अलग होने की दर ज्ञात कीजिए।
कोण θ, 0 < θ < `π/2`, ज्ञात कीजिए जो अपने sine से दोगुनी तेजी से बढ़ता है।
एक खोखले बेलनाकार खोल, जिसकी आंतरिक तथा बाह्य त्रिज्याएँ क्रमश: 3 cm तथा 3.0005 cm हैं, में धातु के आयतन का सन्निकट मान ज्ञात कीजिए।
किसी तरनताल को सफाई के लिए खाली करना है।यदि ताल को बंद करने के t seconds बाद ताल में पानी की मात्रा, लिटर में, L से निरूपित होती है तथा L = 200 (10 – t)2 तो 5 seconds में अंत में पानी कितनी तेजी से बाहर निकल रहा है? प्रथम 5 seconds में पानी के बाहर निकलने की औसत दर क्या है?
x तथा y दो वर्गों की भुजाएँ हैं, इस प्रकार कि y = x – x2 दूसरे वर्ग के क्षेत्रफल में परिवर्तनकी दर पहले वर्ग के क्षेत्रफल के सापेक्ष ज्ञात कीजिए।
सिद्ध कीजिए कि a ≥ 1 के लिए f (x) = `sqrt3` sinx - cosx - 2ax + b, R में हासमान फलन है।
फलन f (x) = x5 – 5x4 + 5x3 – 1 के स्थानीय उच्चिष्ठ, स्थानीय निम्निष्ठ तथा नति परिवर्तन के बिंदुओं को ज्ञात कीजिए। साथ ही संगत स्थानीय उच्चतम तथा स्थानीय निम्नतम मानों को भी ज्ञात कीजिए।
AB किसी वृत्त का एक व्यास है तथा C उसकी परिधि पर कोई बिंदु है। सिद्ध कीजिए कि ∆ ABC का क्षेत्रफल महत्तम उस समय होगा जब वह समद्धिबाहु है।
रेखा x + 3y = 8 के समांतर, वक् 3x2 – y2 = 8 के अभिलंब का समीकरण है।
वक्र y (1 + x2 ) = 2 – x के, उस बिंदु पर, जहाँ यह x-अक्ष को काटती है, स्पर्श रेखा का समीकरण ______
वक्र y = e2x की, बिंदु (0, 1) पर, स्पर्श रेखा x-अक्ष से बिंदु ______
y = x(x – 3)2, x के नीचे दिए हुए मानों के लिए हासमान है,
बहुपद x3 – 18x2 + 96x का, अंतराल [0, 9] में, निम्नतम मान ______
sin x . cos x का उच्चतम मान है ______
f (x) = 2 sin3x + 3 cos3x का मान x = `(5pi)/6`, पर ______
