Advertisements
Advertisements
Question
किसी वृत्त की जीवा की लंबाई 24 सेमी तथा केंद्र से जीवा 5 सेमी दूरी पर है तो वृत्त की त्रिज्या ज्ञात कीजिए?
Options
12 सेमी
13 सेमी
14 सेमी
15 सेमी
Solution
13 सेमी
स्पष्टीकरण:
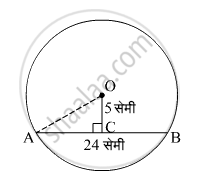
माना कि जीवा AB = 24 सेमी
केंद्र O से जीवा की दूरी 5 सेमी है।
AO वृत्त की त्रिज्या है।
वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है।
तो, AC = CB
ΔAOC में,
OC2 + AC2 = AO2
⇒ 52 + 122 = AO2
⇒ AO2 = 25 + 144 = 169
⇒ AO = 13 सेमी
इस प्रकार, वृत्त की त्रिज्या 13 सेमी है।
APPEARS IN
RELATED QUESTIONS
वृत्त का केन्द्र वृत्त के ______ में स्थित है।
केन्द्र को वृत्त पर किसी बिन्दु से मिलाने वाला रेखाखंड वृत्त की त्रिज्या होती है।
संलग्न आकृति देखकर लिखिए:
बहिर्भाग में एक बिंदु
संलग्न आकृति देखकर लिखिए:
एक वृतखंड
क्या वृत का प्रत्येक जीवा उसका एक व्यास भी होती है?
निम्नलिखित आकृति में, यदि ∠OAB = 40° है, तो ∠ACB बराबर है
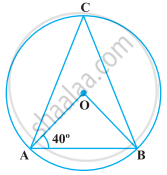
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इस चतुर्भुज के परिगत वृत्त का एक व्यास है तथा ∠ADC = 140° है। तब, ∠BAC बराबर है
O त्रिभुज ABC का परिकेंद्र है तथा D आधार BC का मध्य-बिंदु है। सिद्ध कीजिए कि ∠BOD = ∠A है।
एक वृत्त की दो जीवाएँ AB और AC उसके केंद्र पर क्रमश : 90° और 150° के कोण अंतरित करती हैं। ∠BAC ज्ञात कीजिए, यदि AB और AC केंद्र के विपरीत ओर स्थित हैं।
आकृति में O एक वृत्त का केंद्र है। एक ऐसी जीवा लिखिए, जो व्यास नहीं है।