Advertisements
Advertisements
Question
A square loop MNOP of side 20 cm is placed horizontally in a uniform magnetic field acting vertically downwards as shown in the figure. The loop is pulled with a constant velocity of 20 cm s−1 till it goes out of the field.
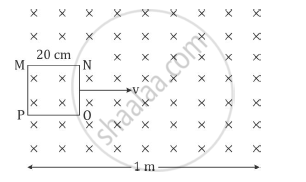
(i) Depict the direction of the induced current in the loop as it goes out of the field. For how long would the current in the loop persist?
(ii) Plot a graph showing the variation of magnetic flux and induced emf as a function of time.
Solution
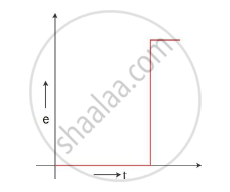
(i)The direction of induced current in the loop as it goes out is depicted in the figure below.
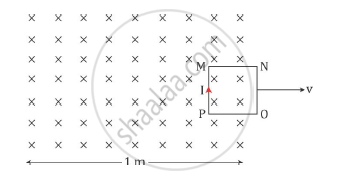
The current will persist till the entire loop comes out of the field. Hence, we have
`t=d/v=(20 cm)/(20 `
Hence, the current will persist for 1 second.
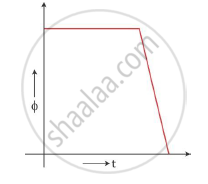
(ii)The magnetic flux in the coil when it is inside the field is constant. This maximum flux is given as Φ = Bla (a is the side of the square loop). This flux will start dropping once the loop comes out of the field and will be zero when it is completely out of the field.
The e.m.f. induced in the coil when it is inside the field is zero as the flux is not changing. When the loop just comes out of the field, the flux change is maximum and the e.m.f. induced is `e=(dphi)/dt=-Bl(db)/(dt)=-Blv` This e.m.f remains constant till the entire loop comes out. When the loop is completely out of the field, the e.m.f. drops to zero again.
APPEARS IN
RELATED QUESTIONS
Draw a schematic sketch of an ac generator describing its basic elements. State briefly its working principle. Show a plot of variation of
(i) Magnetic flux and
(ii) Alternating emf versus time generated by a loop of wire rotating in a magnetic field.
A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from 0 to 20 A in 0.5 s, what is the change of flux linkage with the other coil?
A rectangular coil having 60 turns and area of 0.4m2 is held at right angles to a uniform magnetic field of flux density 5 × 10-5T. Calculate the magnetic flux passing through it.
Answer the following question.
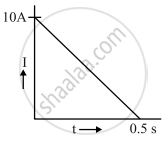
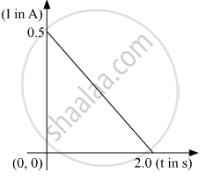
When a conducting loop of resistance 10 Ω and area 10 cm2 is removed from an external magnetic field acting normally, the variation of induced current-I in the loop with time t is as shown in the figure.
Find the
(a) total charge passed through the loop.
(b) change in magnetic flux through the loop
(c) magnitude of the field applied
The magnetic flux linked with a coil of N turns of area of cross-section A held with its plane parallel to the field B is ______.
Two inductors of inductance L each are connected in series with the opposite? magnetic fluxes. The resultant inductance is ______.
A loop, made of straight edges has six corners at A(0, 0, 0), B(L, O, 0) C(L, L, 0), D(0, L, 0) E(0, L, L) and F(0, 0, L). A magnetic field `B = B_o(hati + hatk)`T is present in the region. The flux passing through the loop ABCDEFA (in that order) is ______.
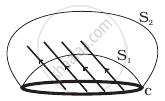
Consider a closed loop C in a magnetic field (Figure). The flux passing through the loop is defined by choosing a surface whose edge coincides with the loop and using the formula φ = B1.dA1 + B2.dA2 +... Now if we chose two different surfaces S1 and S2 having C as their edge, would we get the same answer for flux. Jusity your answer.
In a coil of resistance 100 Ω a current is induced by changing the magnetic flux through it. The variation of current with time is shown in the figure. The magnitude of change in flux through the coil is ______.