Advertisements
Advertisements
Question
Mahendra and Virat are sitting at a distance of 1 m from each other.Their masses are 75 kg and 80 kg respectively. What is the gravitational force between them? (G = 6.67 × 10-11 Nm2/kg2)
Solution
Given: Distance (r) = 1 m, mass (m1) = 75 kg, mass (m2) = 80 kg, gravitational constant (G) = 6.67 × 10-11 Nm2/kg2
To find: Gravitational force (F)
Formula: F = `("Gm"_1"m"_2)/"r"^2`
Calculation: From formula,
F = `(6.67 xx 10^-11 xx 75 xx 80)/1^2`
∴ F = 4.002 × 10-7 N
The gravitational force between Mahendra and Virat is 4.002 × 10-7 N.
APPEARS IN
RELATED QUESTIONS
If the moon attracts the earth, why does the earth not move towards the moon?
What happens to the force between two objects, if the distance between the objects is doubled and tripled?
Choose the correct answer from among the given ones:
For the problem 8.10, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii) e, (iii) f, (iv) g.
Which of the Kepler’s laws of planetary motion led Newton to establish the inverse-square rule for gravitational force between two bodies ?
Can two particles be in equilibrium under the action of their mutual gravitational force? Can three particles be? Can one of the three particles be?
Suppose the gravitational potential due to a small system is k/r2 at a distance r from it. What will be the gravitational field? Can you think of any such system? What happens if there were negative masses?
The weight of an object is more at the poles than at the equator. Is it beneficial to purchase goods at equator and sell them at the pole? Does it matter whether a spring balance is used or an equal-beam balance is used?
Let V and E be the gravitational potential and gravitational field at a distance r from the centre of a uniform spherical shell. Consider the following two statements :
(A) The plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
Three equal masses m are placed at the three corners of an equilateral triangle of side a. Find the force exerted by this system on another particle of mass m placed at (a) the mid-point of a side, (b) at the centre of the triangle.
Two concentric spherical shells have masses M1, M2 and radii R1, R2 (R1 < R2). What is the force exerted by this system on a particle of mass m1 if it is placed at a distance (R1+ R2)/2 from the centre?
The mass of moon is about 0.012 times that of earth and its diameter is about 0.25 times that of earth. The value of G on the moon will be:
State whether the gravitational force between two masses is attractive or repulsive ?
The force of attraction between any two material objects is called __________.
Where will you weigh more: at the centre of the earth or at the surface of the earth?
At what height above the earth's surface would the value of acceleration due to gravity be half of what it is on the surface? Take the radius of earth to be R.
The distance-time values for an object moving along straight line are given below:
| Time (s) | Distance (m) |
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
Solve the following problem.
Find the gravitational force between the Sun and the Earth.
Given Mass of the Sun = 1.99 × 1030 kg
Mass of the Earth = 5.98 × 1024 kg
The average distance between the Earth and the Sun = 1.5 × 1011 m.
For the weight of body of mass 5 kg to be zero on equator of the earth, angular velocity of the earth must be (The radius of earth = 6400 km, acceleration due to gravity = 10 m/s2).
The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
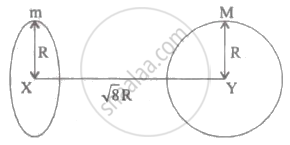
Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If `sqrt8` R is the distance between the centres of a ring (of mass 'm')and a sphere (mass 'M') where both have equal radius 'R'.