Advertisements
Advertisements
Question
निम्न रैखिक समीकरणों के युग्मों को हल कीजिए:
152x - 378y = -74
-378x + 152y = -604
Solution
चूँकि 152x - 378y = -74
⇒ 152x - 378y + 74 = 0 ….(1)
एवं -378x + 152y = -604
⇒ -378x + 152y + 604 = 0 ….(2)
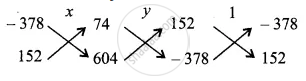
⇒ `x/(-378(604) - 152(74)) = y/(74(-378) - 604(152)) = 1/(152(152) - (-378)(-378))`
⇒ `(-x)/(378(604) + 152(74)) = (-y)/(74(378) + 604(152)) = (-1)/((378)^2 - (152)^2)`
⇒ `x/(378(604) + 152(74)) = y/(74(378) + 604(152)) = 1/((378 + 152) xx (378 - 152))`
⇒ `x/(378(604) + 152(74)) = y/(74(378) + 604(152)) = 1/(530 xx 226`
⇒ `x = (378 xx 604 + 152 xx 74)/(530 xx 226) = (228312 + 11248)/(119780)`
= `239560/119780 = 2`
एवं `y = (74 xx 378 + 604 xx 152)/(530 xx 226)`
= `(27972 + 91808)/(119780) = 119780/119780 = 1`
अतः दत्त समीकरण युग्म का अभीष्ट हल x = 2 एवं y = 1 है।
APPEARS IN
RELATED QUESTIONS
आफ़ताब अपनी पुत्री से कहता है, 'सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था। अब से 3 वर्ष बाद मैं तुमसे केवल तीन गुनी आयु का रह जाऊँगा। (क्या यह मनोरंजक है?)' इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए।
अनुपातों `bb(a_1/a_2, b_1/b_2)` और `(c_1/c_2)` की तुलना कर ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपण रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं:
5x - 4y + 8 = 0
7x + 6y - 9 = 0
अनुपातों `bb(a_1/a_2, b_1/b_2)` और `bb(c_1/c_2)` की तुलना कर ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपण रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं:
9x + 3y + 12 = 0
18x + 6y + 24 = 0
निम्न रैखिक समीकरणों के युग्मों को हल कीजिए:
px + qy = p - q
qx - py = p + q
निम्न रैखिक समीकरणों के युग्मों को हल कीजिए:
ax + by = c
bx + ay = 1 + c
c का वह मान, जिसके लिए समीकरणों cx – y = 2 और 6x – 2y = 3 के युग्म के अपरिमित रूप से अनेक हल होंगे, है ______।
आश्रित रैखिक समीकरणों के युग्म का एक समीकरण –5x + 7y = 2 है दूसरा समीकरण हो ______।
एक अद्वितीय हल x = 2, y = –3 वाले समीकरण का एक युग्म है ______।
यदि x = a और y = b समीकरणों x – y = 2 और x + y = 4, का हल है, तो a और b के मान क्रमश : हैं ______।
4 पेन और 4 पेंसिल बॉक्सों का मूल्य 100 रु है। एक पेन के मूल्य का तीन गुना एक पेंसिल बॉक्स के मूल्य से 15 रु अधिक है। उपरोक्त स्थिति के लिए, रैखिक समीकरणों का एक युग्म बनाइए। एक पेन और एक पेंसिल बॉक्स के मूल्य भी ज्ञात कीजिए।
