Advertisements
Advertisements
Question
प्रत्येक समलंब एक समांतर चतुर्भुज है।
Options
सत्य
असत्य
Solution
यह कथन असत्य है।
स्पष्टीकरण -
समांतर चतुर्भुज में, भुजाओं के दोनों युग्म समांतर होने चाहिए।
तो, एक समलम्ब चतुर्भुज में, भुजाओं का केवल एक युग्म समानांतर होता है। अर्थात यह समांतर चतुर्भुज के लिए शर्तों को पूरा नहीं करता है।
चूँकि एक समलंब में, भुजाओं का केवल एक युग्म समांतर होता है।
APPEARS IN
RELATED QUESTIONS
आकृति में m∠C ज्ञात कीजिए जदि `overline("AB") || overline("DC")` है।

सभी समांतर चतुर्भुज समलंब होते है।
निम्न में से कौन-सी आकृति नीचे लिखे गुणों में से किसी भी गुण को संतुष्ट नहीं करती?
"सभी भुजाएँ बराबर हैं।"
"सभी कोण समकोण हैं।"
"सम्मुख भुजाएँ समान्तर हैं।"
प्रत्येक समचतुर्भुज एक समलंब है।
चार चतुर्भुजों - वर्ग, आयत, समचतुर्भुज और समलंब में से एक अन्य तीन से अपने डिजाइन के कारण कुछ भिन्न हैं। उसे ज्ञात कीजिए और उसका औचित्य दीजिए।
समलंब HARE में, EP और RP क्रमश: ∠E और ∠R के समद्विभाजक हैं। ∠HAR और ∠EHA ज्ञात कीजिए।

एक चतुर्भुज HOPE में, PS और ES क्रमशः ∠P और ∠E के समद्विभाजक हैं। क्या ∠O + ∠H = 2∠PSE है? कारण दीजिए।
एक समलंब RISK की रचना कीजिए, जिसमें RI || KS, RI = 7 cm, IS = 5 cm, RK = 6.5 cm और ∠I = 60∘ है।
एक समलंब ABCD की रचना कीजिए, जिसमें AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm और CD = 9.6 cm है। ∠B और ∠A को मापिए।
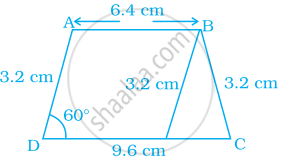
[सिंकेत – दोनों समांतर भुजाओं के अंतर से एक समबाहु त्रिभुज की भुजा प्राप्त होती है।]
आकृति में `square`ABCD में भुजा BC < भुजा AD, भुजा BC || भुजा AD तथा यदि भुजा BA ≅ भुजा CD हो तो सिद्ध कीजिए कि `angle`ABC ≅ `angle`DCB