Advertisements
Advertisements
Question
Represent the given relation by
(a) an arrow diagram
(b) a graph and
(c) a set in roster form, wherever possible
{(x, y) | y = x + 3, x, y are natural numbers < 10}
Solution
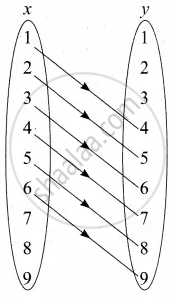
x = {1, 2, 3, 4, 5, 6, 7, 8, 9}
y = {1, 2, 3, 4, 5, 6, 7, 8, 9}
y = x + 3
when x = 1 ⇒ y = 1 + 3 = 4
when x = 2 ⇒ y = 2 + 3 = 5
when x = 3 ⇒ y = 3 + 3 = 6
when x = 4 ⇒ y = 4 + 3 = 7
when x = 5 ⇒ y = 5 + 3 = 8
when x = 6 ⇒ y = 6 + 3 = 9
when x = 7 ⇒ y = 7 + 3 = 10
when x = 8 ⇒ y = 8 + 3 = 11
when x = 9 ⇒ y = 9 + 3 = 12
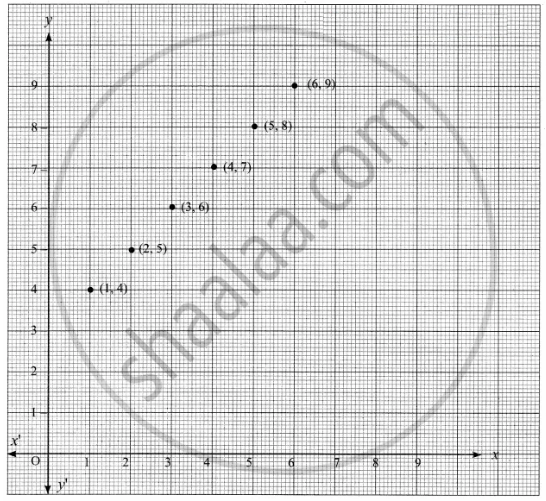
R = {(1, 4) (2, 5) (3, 6) (4, 7) (5, 8) (6, 9)}
(a) Arrow diagram
(b) Graph
(c) Roster form: R = {(1, 4) (2, 5) (3, 6) (4, 7) (5, 8) (6, 9)}
APPEARS IN
RELATED QUESTIONS
A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.
Let A = [1, 2, 3, 4, 5, 6]. Let R be a relation on A defined by {(a, b) : a, b ∈ A, b is exactly divisible by a}
(i) Writer R in roster form
(ii) Find the domain of R
(ii) Find the range of R.
For the relation R1 defined on R by the rule (a, b) ∈ R1 ⇔ 1 + ab > 0. Prove that: (a, b) ∈ R1 and (b , c) ∈ R1 ⇒ (a, c) ∈ R1 is not true for all a, b, c ∈ R.
Let R be a relation on N × N defined by
(a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N
Show that:
(i) (a, b) R (a, b) for all (a, b) ∈ N × N
Let A = [1, 2, 3], B = [1, 3, 5]. If relation R from A to B is given by = {(1, 3), (2, 5), (3, 3)}, Then R−1 is
Write the relation in the Roster Form. State its domain and range
R1 = {(a, a2)/a is prime number less than 15}
Write the relation in the Roster Form. State its domain and range
R5 = {(x, y)/x + y = 3, x, y∈ {0, 1, 2, 3}
Select the correct answer from given alternative.
The relation ">" in the set of N (Natural number) is
Answer the following:
Determine the domain and range of the following relation.
R = {(a, b)/b = |a – 1|, a ∈ Z, IaI < 3}
Answer the following:
Check if R : Z → Z, R = {(a, b)/2 divides a – b} is equivalence relation.
