Advertisements
Advertisements
Question
Represent the given relation by
(a) an arrow diagram
(b) a graph and
(c) a set in roster form, wherever possible
{(x, y) | x = 2y, x ∈ {2, 3, 4, 5}, y ∈ {1, 2, 3, 4}
Solution
x = {2, 3, 4, 5} y = {1, 2, 3, 4}
x = 2y
2y = x
y = `x/2`
If `x = 2 ⇒ y = x/2 = 2/2 = 1`
if `x = 3 ⇒ y = x/2 = 3/2`
If `x = 4 ⇒ y = x/2 = 4/2 = 2`
If `x = 5 ⇒ y = x/2 = 5/2`
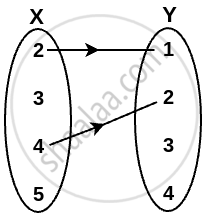
(a) Arrow diagram
(b) Graph
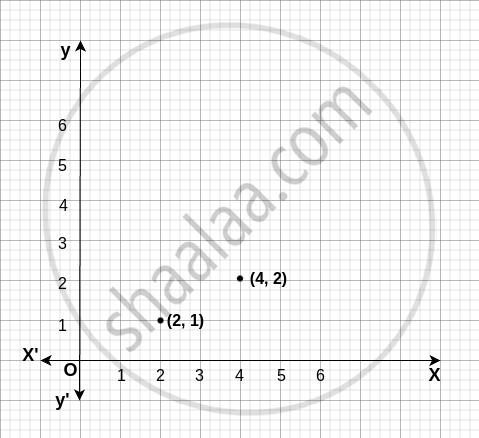
(c) Roster form R = {(2, 1) (4, 2)}
APPEARS IN
RELATED QUESTIONS
The relation f is defined by f(x) = `{(x^2,0<=x<=3),(3x,3<=x<=10):}`
The relation g is defined by g(x) = `{(x^2, 0 <= x <= 2),(3x,2<= x <= 10):}`
Show that f is a function and g is not a function.
Let A = (3, 5) and B = (7, 11). Let R = {(a, b) : a ∈ A, b ∈ B, a − b is odd}. Show that R is an empty relation from A into B.
A relation ϕ from C to R is defined by x ϕ y ⇔ |x| = y. Which one is correct?
If the set A has p elements, B has q elements, then the number of elements in A × B is
Discuss the following relation for reflexivity, symmetricity and transitivity:
Let P denote the set of all straight lines in a plane. The relation R defined by “lRm if l is perpendicular to m”
In the set Z of integers, define mRn if m − n is divisible by 7. Prove that R is an equivalence relation
Choose the correct alternative:
Let R be the set of all real numbers. Consider the following subsets of the plane R × R: S = {(x, y) : y = x + 1 and 0 < x < 2} and T = {(x, y) : x − y is an integer} Then which of the following is true?
Choose the correct alternative:
The number of relations on a set containing 3 elements is
Given R = {(x, y) : x, y ∈ W, x2 + y2 = 25}. Find the domain and Range of R.
If R1 = {(x, y) | y = 2x + 7, where x ∈ R and – 5 ≤ x ≤ 5} is a relation. Then find the domain and Range of R1.
