Advertisements
Advertisements
Question
शीर्ष कोण `2theta` वाला एक समद्धिबाहु त्रिभुज a त्रिज्या वाले किसी वृत्त के अंतर्गत स्थित है। सिद्ध कीजिए कि त्रिभुजं का क्षेत्रफल उच्चतम है। जब `theta = pi/6`
Advertisements
Solution
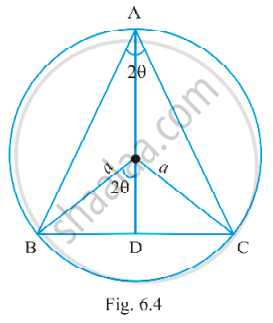
मान लीजिए कि एक समद्धिबाहु त्रिभुज ABC त्रिज्या a वाले किसी वृत्त के अंतर्गत है, इस प्रकार कि AB = AC
AD = AO + OD = a +a cos2`theta` तथा BC = 2 BD
= 2a sin2θ (आकृति 6.4 देखिए)
इसलिए, ∆ ABC का क्षेत्रफल, अर्थात् ∆ = `1 /2` BC . AD
= `1/2 2"a" sin2θ * ("a" + "a" cos2θ)`
= `"a"^2 sin2θ (1 + cos2θ)`
⇒ ∆ = `"a"^2 sin2θ + 1/2 "a"^2 sin4θ`
इसलिए, `("d"∆)/ ("d"θ) = 2"a"^2 cos2θ + 2"a"^2 cos4θ`
= `2"a"^2 (cos2θ + cos4θ)`
`("d"∆)/("d"θ) = 0 ⇒ cos2θ = –cos4θ = cos (π – 4θ)`
इसलिए, `2θ = π – 4θ ⇒ θ = π/6`
`("d"^2∆)/("d"theta)` = 2a2 (–2sin2θ – 4sin4θ) < 0 `(theta = pi/6 "पर")`
अतः त्रिभुज का क्षेत्रफल उच्चतम है, जब `theta = pi/6`
APPEARS IN
RELATED QUESTIONS
अवकलज का प्रयोग करके निम्नलिखित में से सन्निकट मान ज्ञात कीजिए।
(33)-1/5
वक्र y2 = x तथा x2 = y के बीच का प्रतिच्छेद - कोण ज्ञात कीजिए।
वक्र y = cos (x + y), –2π ≤ x ≤ 2π, की उन सभी स्पर्श रेखाओं के समीकरण ज्ञात कीजिए जो रेखा x + 2y = 0 के समांतर हैं।
दो वक्र x3 – 3xy2 + 2 = 0 तथा 3x2 y – y3 = 2
समीकरण x = et . cost, y = et . sint द्वारा प्रदत्त वक्र की t = `pi/4` पर स्पर्श रेखा, x-अक्ष से कोण बनाती है।
वक्र y = sinx के बिंदु (0, 0) पर अभिलंब का समीकरण:
किसी गोले के आयतन के परिवर्तन की दर उसके पृष्ठीय क्षेत्रफल के सापेक्ष, जब उसकी त्रिज्या 2cm है, ______ है।
नमक का एक गोलाकार गेंद पानी में इस प्रकार घुल रहा है कि किसी क्षण उसके आयतन के घटने की दर उसके पृष्ठीय क्षेत्रफल के समानुपाती है। सिद्ध कीजिए कि उसकी त्रिज्या एक अचर दर से घट रही है।
कोण θ, 0 < θ < `π/2`, ज्ञात कीजिए जो अपने sine से दोगुनी तेजी से बढ़ता है।
एक खोखले बेलनाकार खोल, जिसकी आंतरिक तथा बाह्य त्रिज्याएँ क्रमश: 3 cm तथा 3.0005 cm हैं, में धातु के आयतन का सन्निकट मान ज्ञात कीजिए।
x तथा y दो वर्गों की भुजाएँ हैं, इस प्रकार कि y = x – x2 दूसरे वर्ग के क्षेत्रफल में परिवर्तनकी दर पहले वर्ग के क्षेत्रफल के सापेक्ष ज्ञात कीजिए।
सिद्ध कीजिए कि वक्र y2 = 4x तथा x2 + y2 – 6x + 1 = 0 एक दूसरे को बिंदु (1, 2) पर स्पर्श करते हैं।
यदि किसी समकोण त्रिभुज की एक भुजा तथा कर्ण की लंबाईयों का योगफल दिया हुआ है, तो सिद्ध कीजिए कि त्रिभुज का क्षेत्रफल उच्चतम है, जब उनके मध्य का कोण `pi/3` है।
c2 क्षेत्रफल के किसी दिए हुए गत्ते से वर्गाकार आधार का एक खुला हुआ बाक्स बनाना है। सिद्ध कीजिए कि बाक्स का महत्तम आयतन `c^3/(6sqrt3)` घन इकाई है।
भुजा x, 2x और `x/3` किसी आयताकार समांतर षट्फलक तथा एक गोले के पृष्ठीय क्षेत्रफल का योगफल अचर दिया हुआ है। सिद्ध कीजिए कि उनके आयतन का योगफल निम्नतम होगा, यदि x गोले की त्रिज्या के तीन गुने के बराबर है। उनके आयतन के योगफल का निम्नतम मान भी ज्ञात कीजिए।
एक क्षैतिज फर्श पर 5 मीटर लंबी एक सीढ़ी किसी ऊर्ध्वाधर दीवार पर झुकी है।यदि सीढ़ी का ऊपरी सिरा 10 cm/sec, की दर से नीचे की ओर फिसल रहा है तो सीढ़ी तथा फर्श के बीच का कोण, उस समय जब सीढ़ी का निचला सिरा दीवार से 2 मीटर दूर है:
वे बिंदु, जिन पर वक्र y = x3 – 12x + 18 की स्पर्श रेखाएँ x-अक्ष के समांतर हैं,
वक्र y = e2x की, बिंदु (0, 1) पर, स्पर्श रेखा x-अक्ष से बिंदु ______
दो वक्र x3 – 3xy2 + 2 = 0 तथा 3x2 y – y3 – 2 = 0 किस कोण पर प्रतिच्छेद करते हैं:
y = x(x – 3)2, x के नीचे दिए हुए मानों के लिए हासमान है,
फलन f(x) = 4 sin3x – 6 sin2x + 12 sinx + 100 ______
फलन f(x) = tanx – x ______
sin x . cos x का उच्चतम मान है ______
वक्र y = tanx के (0, 0) पर अभिलंब का समीकरण ______ है।
फलन f(x) = `(2x^2 - 1)/x^4`, x > 0, अंतराल में ______ हासमान है।
फलन f(x) = `"a"x + "b"/x` (a > 0, b > 0, x > 0) का निम्नतम मान ______ है।
