Advertisements
Advertisements
प्रश्न
शीर्ष कोण `2theta` वाला एक समद्धिबाहु त्रिभुज a त्रिज्या वाले किसी वृत्त के अंतर्गत स्थित है। सिद्ध कीजिए कि त्रिभुजं का क्षेत्रफल उच्चतम है। जब `theta = pi/6`
Advertisements
उत्तर
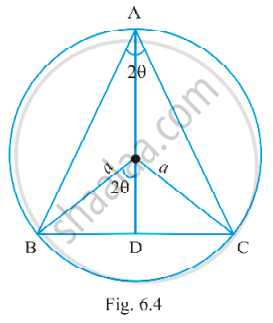
मान लीजिए कि एक समद्धिबाहु त्रिभुज ABC त्रिज्या a वाले किसी वृत्त के अंतर्गत है, इस प्रकार कि AB = AC
AD = AO + OD = a +a cos2`theta` तथा BC = 2 BD
= 2a sin2θ (आकृति 6.4 देखिए)
इसलिए, ∆ ABC का क्षेत्रफल, अर्थात् ∆ = `1 /2` BC . AD
= `1/2 2"a" sin2θ * ("a" + "a" cos2θ)`
= `"a"^2 sin2θ (1 + cos2θ)`
⇒ ∆ = `"a"^2 sin2θ + 1/2 "a"^2 sin4θ`
इसलिए, `("d"∆)/ ("d"θ) = 2"a"^2 cos2θ + 2"a"^2 cos4θ`
= `2"a"^2 (cos2θ + cos4θ)`
`("d"∆)/("d"θ) = 0 ⇒ cos2θ = –cos4θ = cos (π – 4θ)`
इसलिए, `2θ = π – 4θ ⇒ θ = π/6`
`("d"^2∆)/("d"theta)` = 2a2 (–2sin2θ – 4sin4θ) < 0 `(theta = pi/6 "पर")`
अतः त्रिभुज का क्षेत्रफल उच्चतम है, जब `theta = pi/6`
APPEARS IN
संबंधित प्रश्न
अवकलज का प्रयोग करके निम्नलिखित में से सन्निकट मान ज्ञात कीजिए।
`(17/81)^(1/4)`
सिद्ध कीजिए कि `x + 1/x` का स्थानीय उच्चतम मीन उसके स्थानीय निम्नतम मान से कम है।
वक्र `3"y" = 6"x" – 5"x"^3` पर स्थित उस बिंदु का भुज, जिस पर वक्र का अभिलंब मूल बिंदुसे होकर जाता है।
वक्र y2 = x पर वह बिंदु जहाँ स्पर्श रेखा x-अक्ष से `pi/4` कोण बनाती है।
मान लीजिए कि c पर f का द्वितीय अवकलज है, इस प्रकार कि f ′(c) = 0 तथा f ″(c) > 0, तो c पर फलन ______ है।
नमक का एक गोलाकार गेंद पानी में इस प्रकार घुल रहा है कि किसी क्षण उसके आयतन के घटने की दर उसके पृष्ठीय क्षेत्रफल के समानुपाती है। सिद्ध कीजिए कि उसकी त्रिज्या एक अचर दर से घट रही है।
यदि किसी वृत्त का क्षेत्रफल एक समान दर से बढ़ता है, तो सिद्ध कीजिए कि उसका परिमाप (परिधि) उसकी त्रिज्या के व्युत्क्रमानुपाती होता है
किसी घन का आयतन एक अचर दर से बढ़ रहा है। सिद्ध कीजिए कि उसके पृष्ठीय क्षेत्रफल की वृद्धि उसकी भुजा की व्युत्क्रमानुपाती है।
x तथा y दो वर्गों की भुजाएँ हैं, इस प्रकार कि y = x – x2 दूसरे वर्ग के क्षेत्रफल में परिवर्तनकी दर पहले वर्ग के क्षेत्रफल के सापेक्ष ज्ञात कीजिए।
सिद्ध कीजिए कि वक्र y2 = 4x तथा x2 + y2 – 6x + 1 = 0 एक दूसरे को बिंदु (1, 2) पर स्पर्श करते हैं।
वक्र 3x2 – y2 = 8 के उन अभिलम्ब रेखाओं के समीकरण ज्ञात कीजिए, जो रेखा x + 3y = 4 के समांतर हैं।
सिद्ध कीजिए कि रेखा `x/"a" +y/"b"` = 1 , वक्र y = b . e-x/a को उस बिंदु पर स्पर्श करती है जिस पर वक्र y-अक्ष को काटता है।
सिद्ध कीजिए कि f (x) = 2x + cot–1x + log `(sqrt(1+x^2) - x)`, R में वर्धमान फलन है।
सिद्ध किजिए कि f (x) = tan–1(sinx + cosx), अतंराल 0,`pi/4` में एक वर्धमान फलन है।
किस बिंदु पर, वक्र y = – x3 + 3x2 + 9x – 27 की प्रवणता उच्चतम है? उच्चतम प्रवणता भी ज्ञात कीजिए।
सिद्ध कीजिए कि f (x) = sinx + `sqrt3` cosx का उच्चिष्ठ मान x = `pi/6` पर है।
फलन f (x) = x5 – 5x4 + 5x3 – 1 के स्थानीय उच्चिष्ठ, स्थानीय निम्निष्ठ तथा नति परिवर्तन के बिंदुओं को ज्ञात कीजिए। साथ ही संगत स्थानीय उच्चतम तथा स्थानीय निम्नतम मानों को भी ज्ञात कीजिए।
किसी नगर में एक टेलीफोन कंपनी की सूची में 500 ग्राहक हैं और वह प्रत्येक ग्राहक से प्रतिवर्ष 300 रु निश्चित शुल्क वसूलती हैं। कंपनी वार्षिक शुल्क बढ़ाना चाहती है, और ऐसा माना जाता है कि प्रत्येक 1 रु की वृद्धि करने पर एक ग्राहक टेलीफोन सेवा लेना समाप्त कर देगा।ज्ञात कीजिए कि कितनी वृद्धि करने से महत्तम (उच्चतम) लाभ होगा।
यदि सरल रेखा x cosα + y sinα = p वक्र `x^2/"a"^2 + y^2/"b"^2` = 1 को स्पर्श करती है, तो सिद्ध कीजिए कि a2 cos2α + b2 sin2α = p2
वर्गाकार आधार तथा ऊर्ध्वाधर पृष्ठ वाले धातु के किसी बाक्स में 1024 cm3 वस्तु आती है। शीर्ष तथा आधार के पृष्ठों के माल (वस्तु) का मूल्य Rs 5/cm2 है तथा पृष्ठों के मान का मूल्य Rs 2.50/cm2 हैं। बाक्स का निम्नतम मूल्य ज्ञात कीजिए।
वक्र x = t2 + 3t – 8, y = 2t2 – 2t – 5 की, बिंदु (2, -1) पर, स्पर्श रेखा की प्रवणता ______ है।
वह अंतराल, जिसमें फलन f (x) = 2x3 + 9x2 + 12x – 1 हासमान है,
y = x(x – 3)2, x के नीचे दिए हुए मानों के लिए हासमान है,
फलन f(x) = 4 sin3x – 6 sin2x + 12 sinx + 100 ______
निम्नलिखित में से कौन-सा फलन 0, `pi/2` में हासमान है,
यदि x एक वास्तविक संख्या है, तो x2 – 8x + 17 का निम्नतम मान ______
वक् y = –x3 + 3x2 + 9x – 27 की उच्चतम प्रवणता ______
वक् y = 4x2 + 2x – 8 तथा, y = x3 – x + 13 एक दूसरे को बिंदु ______ पर स्पर्श करते हैं।
