Advertisements
Advertisements
प्रश्न
एक क्षैतिज फर्श पर 5 मीटर लंबी एक सीढ़ी किसी ऊर्ध्वाधर दीवार पर झुकी है।यदि सीढ़ी का ऊपरी सिरा 10 cm/sec, की दर से नीचे की ओर फिसल रहा है तो सीढ़ी तथा फर्श के बीच का कोण, उस समय जब सीढ़ी का निचला सिरा दीवार से 2 मीटर दूर है:
विकल्प
`1/10` radian/sec
`1/20` radian/sec
20 radian/sec
10` radian/sec
उत्तर
सही उत्तर `underline(1/20 "radian/sec")` है।
व्याख्या:
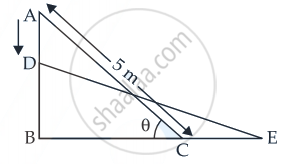
सीढ़ी की लंबाई = 5 m
माना AB = y m and BC = x m
∴ दायीं ओर ΔABC में,
AB2 + BC2 = AC2
⇒ x2 + y2 = (5)2
⇒ x2 + y2 = 25
दोनों पक्षों को w.r.t x, में विभेदित करते हुए, हमारे पास है
`2x * "dx"/"dt" + 2y * "dy"/"dt"` = 0
⇒ `x "dx"/"dt" + y * "dy"/"dt"` = 0
⇒ `2 * "dx"/"dt" + y xx (-0.1)` = 0 ....[∵ x = 2m]
⇒ `2 * "dx"/"dt" + sqrt(25 - x^2) xx (-0.1)` = 0
⇒ `2 * "dx"/"dt" + sqrt(25 - 4) xx (-0.1)` = 0
⇒ `2 * "dx"/"dt" - sqrt(21)/10` = 0
⇒ `"dx"/"dt" = sqrt(21)/20`
अब cos θ = `"BC"/"AC"` ....(θ radian में है)
⇒ cos θ = `x/5`
दोनों पक्षों में अंतर करना w.r.t. t, हमें मिलता है
`"d"/"dt" cos theta = 1/5 * "dx"/"dt"`
⇒ `- sin theta ("d"theta)/"dt" = 1/5 * sqrt(21)/20`
⇒ `("d"theta)/"dt" = sqrt(21)/100 xx (- 1/sin theta)`
= `sqrt(21)/100 xx -(1/("AB"/"AC"))`
= `- sqrt(21)/100 xx "AC"/"AB"`
= `- sqrt(21)/100 xx 5/sqrt(21)`
= `- 1/20` radian/sec
[(–) चिन्ह कोण के परिवर्तन में कमी दर्शाता है]
इसलिए, अभीष्ट दर = `1/20` radian/sec
APPEARS IN
संबंधित प्रश्न
अवकलज का प्रयोग करके निम्नलिखित में से सन्निकट मान ज्ञात कीजिए।
`(17/81)^(1/4)`
सिद्ध कीजिए कि फलन f(x) = 4x3 – 18x2 + 27x – 7 का कोई उच्चिष्ठ अथवा निम्निष्ठ नहीं है।
किसी शांकवीय बर्तन के शीर्ष के एक छोटे छिद्र से, जिसका अक्ष ऊर्घ्वाधर है, पानी 1 cu cm/sec की दर से बह रहा है। बर्तन में पानी के सतह की तिर्यक ऊँचाई के घटने की दर उस समय ज्ञात कीजिए जब तिर्यक ऊँचाई 4 cm हैं। शांकवीय बर्तन का शीर्ष कोण `pi/6` है।
f(x) = secx + log cos2x, 0 < x < 2π का उच्चतम तथा निम्नतम मान ज्ञात कीजिए।
वक्र `3"y" = 6"x" – 5"x"^3` पर स्थित उस बिंदु का भुज, जिस पर वक्र का अभिलंब मूल बिंदुसे होकर जाता है।
समीकरण x = et . cost, y = et . sint द्वारा प्रदत्त वक्र की t = `pi/4` पर स्पर्श रेखा, x-अक्ष से कोण बनाती है।
वक्र y = sinx के बिंदु (0, 0) पर अभिलंब का समीकरण:
वक्र y2 = x पर वह बिंदु जहाँ स्पर्श रेखा x-अक्ष से `pi/4` कोण बनाती है।
मान लीजिए कि c पर f का द्वितीय अवकलज है, इस प्रकार कि f ′(c) = 0 तथा f ″(c) > 0, तो c पर फलन ______ है।
यदि f (x) = sinx तो अंतराल `[(-pi)/2, pi/2]` में f का निम्निष्ठ मान ______ है।
किसी गोले के आयतन के परिवर्तन की दर उसके पृष्ठीय क्षेत्रफल के सापेक्ष, जब उसकी त्रिज्या 2cm है, ______ है।
यदि किसी वृत्त का क्षेत्रफल एक समान दर से बढ़ता है, तो सिद्ध कीजिए कि उसका परिमाप (परिधि) उसकी त्रिज्या के व्युत्क्रमानुपाती होता है
एक पतंग 151.5 cm की ऊंचाई पर क्षैतिज दिशा में गतिमान है। यदि पतंग की चाल 10 m/s है, तो डोरी को कितनी तेजी से छोड़ा जा रहा है, जब उसकी दूरी पतंग उड़ाने वाले लड़के से 250 cm है? लड़के की ऊंचाई 1.5 m है।
(1.999)5 का सन्निकट मान ज्ञात कीजिए।
सिद्ध कीजिए कि वक्र xy = 4 तथा x2 + y2 = 8, एक दूसरे को स्पर्श करते हैं।
वक्र `sqrt(x) + sqrt(y) = 4` उस बिंदु के निर्देशांक ज्ञात कीजिए, जिस पर स्पर्श रेखा का अक्षों से झुकाव समान है।
किसी नगर में एक टेलीफोन कंपनी की सूची में 500 ग्राहक हैं और वह प्रत्येक ग्राहक से प्रतिवर्ष 300 रु निश्चित शुल्क वसूलती हैं। कंपनी वार्षिक शुल्क बढ़ाना चाहती है, और ऐसा माना जाता है कि प्रत्येक 1 रु की वृद्धि करने पर एक ग्राहक टेलीफोन सेवा लेना समाप्त कर देगा।ज्ञात कीजिए कि कितनी वृद्धि करने से महत्तम (उच्चतम) लाभ होगा।
भुजा x, 2x और `x/3` किसी आयताकार समांतर षट्फलक तथा एक गोले के पृष्ठीय क्षेत्रफल का योगफल अचर दिया हुआ है। सिद्ध कीजिए कि उनके आयतन का योगफल निम्नतम होगा, यदि x गोले की त्रिज्या के तीन गुने के बराबर है। उनके आयतन के योगफल का निम्नतम मान भी ज्ञात कीजिए।
बिंदु (0, 0) पर वक्र y = `x^(1/5)` की ______
दो वक्र x3 – 3xy2 + 2 = 0 तथा 3x2 y – y3 – 2 = 0 किस कोण पर प्रतिच्छेद करते हैं:
मान लीजिए कि f : R → R, f (x) = 2x + cosx द्वारा परिभाषित है, तो f ______
फलन f(x) = 4 sin3x – 6 sin2x + 12 sinx + 100 ______
फलन f(x) = tanx – x ______
फलन f (x) = 2x3 – 3x2 – 12x + 4 के ______
वक् y = –x3 + 3x2 + 9x – 27 की उच्चतम प्रवणता ______
वक् y = 4x2 + 2x – 8 तथा, y = x3 – x + 13 एक दूसरे को बिंदु ______ पर स्पर्श करते हैं।
वक्र y = tanx के (0, 0) पर अभिलंब का समीकरण ______ है।
