Advertisements
Advertisements
Question
Show that for a material with refractive index `µ ≥ sqrt(2)`, light incident at any angle shall be guided along a length perpendicular to the incident face.
Solution
Let the ray incident on face AB at angle i, after refraction, it travels along PQ and then interact with face AC which is perpendicular to the incident face.
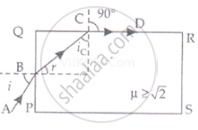
`u = 1/(sin i_c)` .....(Snell's law at c)
`Sin i_c 1/mu [sin i_c = 1/mu]`
`sin(90 - r) ≥ 1/mu` ......[∵ r + 90° + ic = 180]
`cos r ≥ 1/mu`
`cos^2 r ≥ 1/mu^2` ......(Squaring both sides)
`- cos^2 r ≤ 1/mu^2`
`1 - cos^2r ≤ 1 - 1/mu^2`
`sin^2r ≤ 1 - 1/mu^2` ......(I)
`sin i/sinr = mu` .....(By snell's law)
`sin i = mu sin r`
Or `sin^2i = mu^2 sin^2r` ......(Squaring both sides)
`1/mu^2 sin^2i = sin^2r` ......(II)
Put (II) in (I)
`1/mu^2 sin^2i ≤ 1 - 1/mu^2`
`sin^2i ≤ mu^2 - 1` ......[On multiplying by μ2 on both sides]
For smallest angle i.e., i = 90°
∴ `sin^2 90° ≤ mu^2 - 1` ......`[∵ mu ≤ sqrt(2)]`
`1 + 1 ≤ mu^2`
`2 ≤ mu^2`
Taking square root
`sqrt(2) ≤ mu` Hence proved.
APPEARS IN
RELATED QUESTIONS
Is the formula "Real depth/Apparent depth = μ" valid if viewed from a position quite away from the normal?
If the light moving in a straight line bends by a small but fixed angle, it may be a case of
(a) reflection
(b) refraction
(c) diffraction
(d) dispersion.
A vessel contains water up to a height of 20 cm and above it an oil up to another 20 cm. The refractive indices of the water and the oil are 1.33 and 1.30 respectively. Find the apparent depth of the vessel when viewed from above.
Consider the situation in figure. The bottom of the pot is a reflecting plane mirror, S is a small fish and T is a human eye. Refractive index of water is μ. (a) At what distance(s) from itself will the fish see the image(s) of the eye? (b) At what distance(s) from itself will the eye see the image(s) of the fish.

A converging beam of light travelling in air converges at a point P as shown in the figure. When a glass sphere of refractive index 1 . 5 is introduced in between the path of the beam, calculate the new position of the image. Also draw the ray diagram for the image formed.
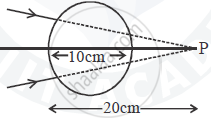
A converging beam of light traveling in air converges at a point P as shown in the figure. When a glass sphere of refractive index 1⋅5 is introduced in between the path of the beam, calculate the new position of, the image. Also, draw the ray diagram for the image formed.
What is critical angle and total internal reflection?
What is looming?
What is Snell’s window?
How does an endoscope work?
