Advertisements
Advertisements
Question
Show that the tangent of an angle between the lines \[\frac{x}{a} + \frac{y}{b} = 1 \text { and } \frac{x}{a} - \frac{y}{b} = 1\text { is } \frac{2ab}{a^2 - b^2}\].
Solution
We have
\[\frac{x}{a} + \frac{y}{b} = 1 \text { and } \frac{x}{a} - \frac{y}{b} = 1\]
\[ \Rightarrow \frac{y}{b} = - \frac{x}{a} + 1 \text { and } \frac{y}{b} = \frac{x}{a} - 1\]
\[ \Rightarrow y = - \frac{b}{a}x + b \text { and} y = \frac{b}{a} - b\]
The slopes of the two lines are \[- \frac{b}{a}\text { and } \frac{b}{a}\]
Now, the tangent of an angle between the lines is given by
\[\frac{\frac{b}{a} + \frac{b}{a}}{1 - \frac{b}{a} \times \frac{b}{a}}\]
\[ = \frac{\frac{2b}{a}}{\frac{a^2 - b^2}{a^2}}\]
\[ = \frac{2ab}{a^2 - b^2}\]
APPEARS IN
RELATED QUESTIONS
The slope of a line is double of the slope of another line. If tangent of the angle between them is `1/3`, find the slopes of the lines.
Find the equation of a line drawn perpendicular to the line `x/4 + y/6 = 1`through the point, where it meets the y-axis.
Find the equation of the lines through the point (3, 2) which make an angle of 45° with the line x –2y = 3.
Find the slope of the lines which make the following angle with the positive direction of x-axis:
\[- \frac{\pi}{4}\]
Find the slope of the lines which make the following angle with the positive direction of x-axis:
\[\frac{2\pi}{3}\]
State whether the two lines in each of the following are parallel, perpendicular or neither.
Through (5, 6) and (2, 3); through (9, −2) and (6, −5)
State whether the two lines in each of the following is parallel, perpendicular or neither.
Through (6, 3) and (1, 1); through (−2, 5) and (2, −5)
Using the method of slope, show that the following points are collinear A (16, − 18), B (3, −6), C (−10, 6) .
What can be said regarding a line if its slope is positive ?
Show that the line joining (2, −5) and (−2, 5) is perpendicular to the line joining (6, 3) and (1, 1).
Without using Pythagoras theorem, show that the points A (0, 4), B (1, 2) and C (3, 3) are the vertices of a right angled triangle.
Consider the following population and year graph:
Find the slope of the line AB and using it, find what will be the population in the year 2010.
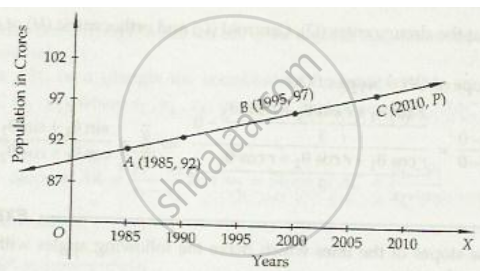
Find the angle between the X-axis and the line joining the points (3, −1) and (4, −2).
Find the equation of a straight line with slope 2 and y-intercept 3 .
Find the equation of a line which is perpendicular to the line joining (4, 2) and (3, 5) and cuts off an intercept of length 3 on y-axis.
Find the coordinates of the orthocentre of the triangle whose vertices are (−1, 3), (2, −1) and (0, 0).
If the image of the point (2, 1) with respect to a line mirror is (5, 2), find the equation of the mirror.
Find the angles between the following pair of straight lines:
3x + 4y − 7 = 0 and 4x − 3y + 5 = 0
The acute angle between the medians drawn from the acute angles of a right angled isosceles triangle is
The angle between the lines 2x − y + 3 = 0 and x + 2y + 3 = 0 is
The medians AD and BE of a triangle with vertices A (0, b), B (0, 0) and C (a, 0) are perpendicular to each other, if
The coordinates of the foot of the perpendicular from the point (2, 3) on the line x + y − 11 = 0 are
If x + y = k is normal to y2 = 12x, then k is ______.
The line passing through (– 2, 0) and (1, 3) makes an angle of ______ with X-axis.
Find the equation of the straight line passing through (1, 2) and perpendicular to the line x + y + 7 = 0.
If the line joining two points A(2, 0) and B(3, 1) is rotated about A in anticlock wise direction through an angle of 15°. Find the equation of the line in new position.
If the slope of a line passing through the point A(3, 2) is `3/4`, then find points on the line which are 5 units away from the point A.
Find the equation of the line passing through the point (5, 2) and perpendicular to the line joining the points (2, 3) and (3, – 1).
The tangent of angle between the lines whose intercepts on the axes are a, – b and b, – a, respectively, is ______.
The coordinates of the foot of perpendiculars from the point (2, 3) on the line y = 3x + 4 is given by ______.
Equations of the lines through the point (3, 2) and making an angle of 45° with the line x – 2y = 3 are ______.
The points (3, 4) and (2, – 6) are situated on the ______ of the line 3x – 4y – 8 = 0.
If the vertices of a triangle have integral coordinates, then the triangle can not be equilateral.
The vertex of an equilateral triangle is (2, 3) and the equation of the opposite side is x + y = 2. Then the other two sides are y – 3 = `(2 +- sqrt(3)) (x - 2)`.
The line `x/a + y/b` = 1 moves in such a way that `1/a^2 + 1/b^2 = 1/c^2`, where c is a constant. The locus of the foot of the perpendicular from the origin on the given line is x2 + y2 = c2.
