Advertisements
Advertisements
Question
Solve each of the following system of equations in R. \[\frac{4}{x + 1} \leq 3 \leq \frac{6}{x + 1}, x > 0\]
Solution
\[\frac{4}{x + 1} \leq 3 \leq \frac{6}{x + 1}, x > 0\]
\[ \Rightarrow \frac{4}{x + 1} \leq 3 and 3 \leq \frac{6}{x + 1}\]
\[\text{ Now }, \]
\[\frac{4}{x + 1} \leq 3\]
\[ \Rightarrow \frac{4}{x + 1} - 3 \leq 0 \]
\[ \Rightarrow \frac{4 - 3x - 3}{x + 1} \leq 0 \]
\[ \Rightarrow \frac{1 - 3x}{x + 1} \leq 0\]
\[ \Rightarrow \frac{3x - 1}{x + 1} \geq 0\]
\[ \Rightarrow x \in \left( - \infty , - 1 \right) \cup [\frac{1}{3}, \infty )\]
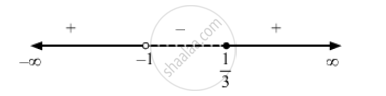
Thus, the solution set of the inequation is \[\left( - \infty , - 1 \right) \cup [\frac{1}{3}, \infty )\]
\[\text{ And } \]
\[\frac{6}{x + 1} \geq 3\]
\[ \Rightarrow \frac{6}{x + 1} - 3 \geq 0\]
\[ \Rightarrow \frac{6 - 3x - 3}{x + 1} \geq 0\]
\[ \Rightarrow \frac{3 - 3x}{x + 1} \geq 0\]
\[ \Rightarrow \frac{3x - 3}{x + 1} \leq 0\]
\[ \Rightarrow x \in ( - 1, 1]\]
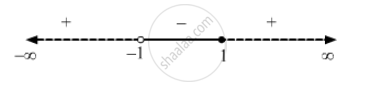
Thus, the solution set of the inequation is \[( - 1, 1]\]
The common values of x in both the inequation is \[\left[ \frac{1}{3}, 1 \right]\]
Hence, the solution set of both the inequation is \[\left[ \frac{1}{3}, 1 \right]\]
APPEARS IN
RELATED QUESTIONS
Solve: −4x > 30, when x ∈ Z
Solve: 4x − 2 < 8, when x ∈ N
x + 5 > 4x − 10
\[2\left( 3 - x \right) \geq \frac{x}{5} + 4\]
\[\frac{2\left( x - 1 \right)}{5} \leq \frac{3\left( 2 + x \right)}{7}\]
\[\frac{x - 1}{3} + 4 < \frac{x - 5}{5} - 2\]
\[\frac{2x + 3}{4} - 3 < \frac{x - 4}{3} - 2\]
\[\frac{5 - 2x}{3} < \frac{x}{6} - 5\]
\[\frac{2x + 3}{5} - 2 < \frac{3\left( x - 2 \right)}{5}\]
\[\frac{x - 1}{x + 3} > 2\]
Solve each of the following system of equations in R.
3x − 6 > 0, 2x − 5 > 0
Solve each of the following system of equations in R.
3x − 1 ≥ 5, x + 2 > −1
Solve each of the following system of equations in R.
2 (x − 6) < 3x − 7, 11 − 2x < 6 − x
Solve each of the following system of equations in R.
\[\frac{2x - 3}{4} - 2 \geq \frac{4x}{3} - 6, 2\left( 2x + 3 \right) < 6\left( x - 2 \right) + 10\]
Solve the following system of equation in R.
\[\frac{2x + 1}{7x - 1} > 5, \frac{x + 7}{x - 8} > 2\]
Solve each of the following system of equations in R.
\[0 < \frac{- x}{2} < 3\]
Solve
\[\left| \frac{3x - 4}{2} \right| \leq \frac{5}{12}\]
Solve \[\frac{\left| x + 2 \right| - x}{x} < 2\]
Solve \[\frac{\left| x - 2 \right| - 1}{\left| x - 2 \right| - 2} \leq 0\]
Mark the correct alternative in each of the following:
If x and a are real numbers such that a\[>\]0 and \\left| x \right|\]\[>\]a, then
Mark the correct alternative in each of the following:
If \[\frac{\left| x - 2 \right|}{x - 2}\]\[\geq\] then
Solve the inequality, 3x – 5 < x + 7, when x is a whole number.
Solve |3 – 4x| ≥ 9.
Solve 1 ≤ |x – 2| ≤ 3.
If |x + 3| ≥ 10, then ______.
If –x ≤ –4, then 2x ______ 8.
If |3x – 7| > 2, then x ______ `5/3` or x ______ 3.
Given that x, y and b are real numbers and x < y, b < 0, then ______.
If x is a real number and |x| < 3, then ______.
State which of the following statement is True or False.
If x < –5 and x < –2, then x ∈ (–∞, –5)
If x < –5 and x > 2, then x ∈ (– 5, 2)
If p > 0 and q < 0, then p – q ______ p.
