Question

Solve each of the following system of equations in R. \[\frac{4}{x + 1} \leq 3 \leq \frac{6}{x + 1}, x > 0\]

Answer 1

\[\frac{4}{x + 1} \leq 3 \leq \frac{6}{x + 1}, x > 0\]
\[ \Rightarrow \frac{4}{x + 1} \leq 3 and 3 \leq \frac{6}{x + 1}\]
\[\text{ Now }, \]
\[\frac{4}{x + 1} \leq 3\]
\[ \Rightarrow \frac{4}{x + 1} - 3 \leq 0 \]
\[ \Rightarrow \frac{4 - 3x - 3}{x + 1} \leq 0 \]
\[ \Rightarrow \frac{1 - 3x}{x + 1} \leq 0\]
\[ \Rightarrow \frac{3x - 1}{x + 1} \geq 0\]
\[ \Rightarrow x \in \left( - \infty , - 1 \right) \cup [\frac{1}{3}, \infty )\]

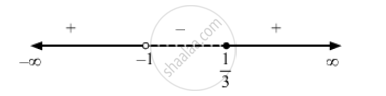
Thus, the solution set of the inequation is \[\left( - \infty , - 1 \right) \cup [\frac{1}{3}, \infty )\]

\[\text{ And } \]
\[\frac{6}{x + 1} \geq 3\]
\[ \Rightarrow \frac{6}{x + 1} - 3 \geq 0\]
\[ \Rightarrow \frac{6 - 3x - 3}{x + 1} \geq 0\]
\[ \Rightarrow \frac{3 - 3x}{x + 1} \geq 0\]
\[ \Rightarrow \frac{3x - 3}{x + 1} \leq 0\]
\[ \Rightarrow x \in ( - 1, 1]\] 

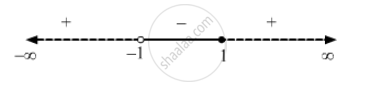
Thus, the solution set of the inequation is \[( - 1, 1]\] 

The common values of x in both the inequation is \[\left[ \frac{1}{3}, 1 \right]\] 

Hence, the solution set of both the inequation is \[\left[ \frac{1}{3}, 1 \right]\]