Advertisements
Advertisements
Question
Solve the following simultaneous equation.
2x + y = -2 ; 3x - y = 7
Solution
2x + y = -2 ...(I)
3x - y = 7 ...(II)
Adding (I) and (II)
5x = 5
⇒ x = 1
Putting the value of x in (I)
2 × 1 + y = -2
⇒ 2 + y = -2
⇒ y = - 4
APPEARS IN
RELATED QUESTIONS
Solve the following system of linear equations by applying the method of elimination by equating the coefficients
(i)4x – 3y = 4
2x + 4y = 3
(ii)5x – 6y = 8
3x + 2y = 6
Solve the following system of linear equations by using the method of elimination by equating the coefficients √3x – √2y = √3 = ; √5x – √3y = √2
Solve for x and y : `\frac { ax }{ b } – \frac { by }{ a } = a + b ; ax – by = 2ab`
Sanjay gets fixed monthly income. Every year there is a certain increment in his salary. After 4 years, his monthly salary was Rs. 4500 and after 10 years his monthly salary became 5400 rupees, then find his original salary and yearly increment.
The difference between an angle and its complement is 10° find measure of the larger angle.
Complete the activity.
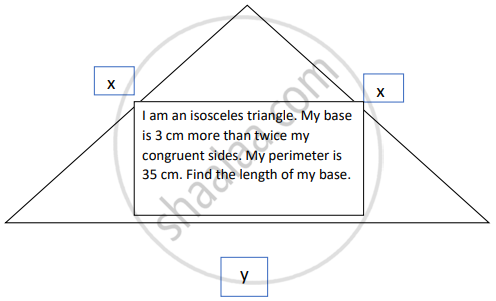
The semi perimeter of a rectangular shape garden is 36 m. The length of the garden is 4 m more than its breadth. Find the length and the breadth of the garden
The angles of a triangle are x, y and 40°. The difference between the two angles x and y is 30°. Find x and y.
The angles of a cyclic quadrilateral ABCD are ∠A = (6x + 10)°, ∠B = (5x)°, ∠C = (x + y)°, ∠D = (3y – 10)°. Find x and y, and hence the values of the four angles.
Read the following passage:
Two schools 'P' and 'Q' decided to award prizes to their students for two games of Hockey ₹ x per student and Cricket ₹ y per student. School 'P' decided to award a total of ₹ 9,500 for the two games to 5 and 4 Students respectively; while school 'Q' decided to award ₹ 7,370 for the two games to 4 and 3 students respectively. |
Based on the above information, answer the following questions:
- Represent the following information algebraically (in terms of x and y).
- (a) What is the prize amount for hockey?
OR
(b) Prize amount on which game is more and by how much? - What will be the total prize amount if there are 2 students each from two games?
