Advertisements
Advertisements
Question
Suppose that the particle is an electron projected with velocity vx = 2.0 × 106 m s−1. If E between the plates separated by 0.5 cm is 9.1 × 102 N/C, where will the electron strike the upper plate? (|e| = 1.6 × 10−19 C, me = 9.1 × 10−31 kg)
Solution
Velocity of the particle, vx = 2.0 × 106 m/s
Separation of the two plates, d = 0.5 cm = 0.005 m
Electric field between the two plates, E = 9.1 × 102 N/C
Charge on an electron, q = 1.6 × 10−19 C
Mass of an electron, me = 9.1 × 10−31 kg
Let the electron strike the upper plate at the end of plate L, when deflection is s.
Therefore,
`"s" = ("qEL"^2)/(2"mv"_"x"^2)`
`"L" = sqrt((2"dmv"_"x"^2)/("qE"))`
= `sqrt((2 xx 0.005 xx 9.1 xx 10^-31 xx (2.0 xx 10^6)^2)/(1.6 xx 10^-10 xx 9.1 xx 10^2))`
= `sqrt(0.025 xx 10^-2)`
= `sqrt(2.5 xx 10^-4)`
= `1.6xx10^-2` m
= 1.6 cm
Therefore, the electron will strike the upper plate after travelling 1.6 cm.
APPEARS IN
RELATED QUESTIONS
Check that the ratio ke2/G memp is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?
A particle of mass m and charge (−q) enters the region between the two charged plates initially moving along x-axis with speed vx (like particle 1 in the fig.). The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL2/(2m`"v"_"x"^2`).

Find the dimensional formula of ε0.
A charge of 1.0 C is placed at the top of your college building and another equal charge at the top of your house. Take the separation between the two charges to be 2.0 km. Find the force exerted by the charges on each other. How many times your weight is this force?
Two charged particles are placed 1.0 cm apart. What is the minimum possible magnitude of the electric force acting on each charge?
Suppose an attractive nuclear force acts between two protons which may be written as F=Ce−kr/r2. Write down the dimensional formulae and appropriate SI units of C and k.
Suppose an attractive nuclear force acts between two protons which may be written as F=Ce−kr/r2. Suppose that k = 1 fermi−1 and that the repulsive electric force between the protons is just balanced by the attractive nuclear force when the separation is 5 fermi. Find the value of C.
Two identical pith balls are charged by rubbing one against the other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. In equilibrium, the separation between the balls is 3 cm. Find the mass of each ball and the tension in the strings. The charge on each ball has a magnitude 2.0 × 10−8 C.
Two small spheres, each with a mass of 20 g, are suspended from a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the separation between the balls at equilibrium is found to be 4 cm. Find the charge on each sphere.
How much work has to be done in assembling three charged particles at the vertices of an equilateral triangle, as shown in the figure?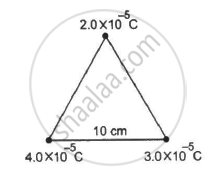
Solve numerical example.
Three equal charges of 10×10-8 C respectively, each located at the corners of a right triangle whose sides are 15 cm, 20 cm, and 25cm respectively. Find the force exerted on the charge located at the 90° angle.
Write down Coulomb’s law in vector form and mention what each term represents.
The force between two charges 0.06 m apart is 5 N. If each charge is moved towards the other by 0.01 m, then the force between them will become ____________.
The ratio of the forces between two small spheres with constant charge (a) in air (b) in a medium of dielectric constant K is ______.
Two identical thin rings, each of radius a meter, are coaxially placed at a distance R meter apart. If Q1 coulomb and Q2 coulomb are respectively the charges uniformly spread on the two rings, the work done in moving a charge q coulomb from the centre of one ring to that of the other is ______.
Identify the wrong statement in the following.
Coulomb's law correctly describes the electric force that ______
According to Coulomb's law, which is the correct relation for the following figure?

