Advertisements
Advertisements
Question
The abscissa of the point of intersection of the less than type and of the more than type cumulative frequency curves of a grouped data gives its ______.
Options
Mean
Median
Mode
All the three above
Solution
The abscissa of the point of intersection of the less than type and of the more than type cumulative frequency curves of a grouped data gives its median.
Explanation:
Since, the intersection point of less than ogive and more than ogive gives the median on the abscissa
The abscissa of the point of intersection of the less than type and of the more than type cumulative frequency curves of a grouped data gives its
APPEARS IN
RELATED QUESTIONS
For a certain frequency distribution, the value of mean is 20 and mode is 11. Find the value of median.
The following table gives the frequency distribution of married women by age at marriage:
| Age (in years) | Frequency |
| 15-19 | 53 |
| 20-24 | 140 |
| 25-29 | 98 |
| 30-34 | 32 |
| 35-39 | 12 |
| 40-44 | 9 |
| 45-49 | 5 |
| 50-54 | 3 |
| 55-59 | 3 |
| 60 and above | 2 |
Calculate the median and interpret the results.
The weights (in kg) of 10 students of a class are given below:
21, 28.5, 20.5, 24, 25.5, 22, 27.5, 28, 21 and 24.
Find the median of their weights.
Estimate the median for the given data by drawing an ogive:
| Class | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Frequency | 4 | 9 | 15 | 14 | 8 |
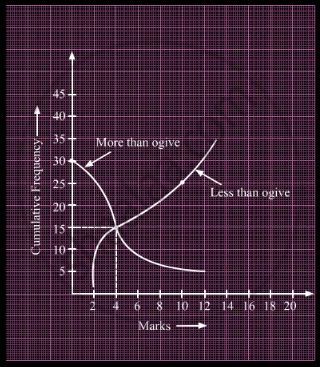
What is the value of the median of the data using the graph in the following figure of less than ogive and more than ogive?
If the difference of Mode and Median of a data is 24, then the difference of median and mean is ______.
Find the median of the following frequency distribution:
| x | 10 | 11 | 12 | 13 | 14 | 15 |
| f | 1 | 4 | 7 | 5 | 9 | 3 |
|
Yoga is an ancient practice which is a form of meditation and exercise. By practising yoga, we not even make our body healthy but also achieve inner peace and calmness. The International Yoga Day is celebrated on the 21st of June every year since 2015.
|
| Age Group | 15 – 25 | 25 – 35 | 35 – 45 | 45 –55 | 55 –65 | 65 –75 | 75 – 85 |
| Number of People |
8 | 10 | 15 | 25 | 40 | 24 | 18 |
Based on the above, find the following:
- Find the median age of people enrolled for the camp.
- If x more people of the age group 65 – 75 had enrolled for the camp, the mean age would have been 58. Find the value of x.
The median of the following frequency distribution is 35. Find the value of x.
| Class: | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Frequency: | 6 | 3 | x | 12 | 19 |
The median of first 10 natural numbers is ______.

