Advertisements
Advertisements
Question
The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution:
| Profit (in lakhs in Rs) | Number of shops (frequency) |
| More than or equal to 5 More than or equal to 10 More than or equal to 15 More than or equal to 20 More than or equal to 25 More than or equal to 30 More than or equal to 35 |
30 28 16 14 10 7 3 |
Draw both ogives for the above data and hence obtain the median.
Solution
Firstly, we prepare the cumulative frequency table for less than type.
Profit (In lakh in Rs.) |
No. of shops (frequency) |
Profit (less than) |
Cumulative frequency |
Suitable points |
| 5-10 | 2 | 10 | 2 | (10, 2) |
| 10-15 | 12 | 15 | 14 | (15, 14) |
| 15-20 | 2 | 20 | 16 | (20, 16) |
| 20-25 | 4 | 25 | 20 | (25, 20) |
| 25-30 | 3 | 30 | 23 | (30, 23) |
| 30-35 | 4 | 35 | 27 | (35, 27) |
| 35-40 | 3 | 40 | 30 | (40, 30) |
Again, prepare the cumulative frequency table for more than type.
Profit (In lakh in Rs.) |
No. of shops (frequency) |
Profit (more than) |
Cumulative |
Suitable |
| 5-10 | 2 | 5 | 30 | (5, 30) |
| 10-15 | 12 | 10 | 28 | (10, 28) |
| 15-20 | 2 | 15 | 16 | (15, 16) |
| 20-25 | 4 | 20 | 14 | (20, 14) |
| 25-30 | 3 | 25 | 10 | (25, 10) |
| 30-35 | 4 | 30 | 7 | (30, 7) |
| 35-40 | 3 | 35 | 3 | (35, 3) |
Now, “more than ogive” and “less than ogive” can be drawn as follows:
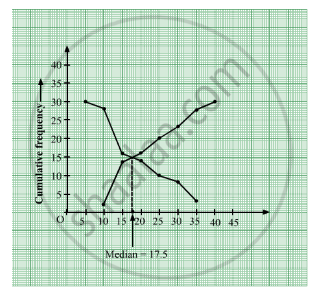
The x-coordinate of the point of intersection of the “more-than ogive” and “less-than ogive” gives the median of the given distribution..
So, the corresponding median is Rs 17.5 lakh.
APPEARS IN
RELATED QUESTIONS
The daily wages of 80 workers in a project are given below.
| Wages (in Rs.) |
400-450 | 450-500 | 500-550 | 550-600 | 600-650 | 650-700 | 700-750 |
| No. of workers |
2 | 6 | 12 | 18 | 24 | 13 | 5 |
Use a graph paper to draw an ogive for the above distribution. (Use a scale of 2 cm = Rs. 50 on x-axis and 2 cm = 10 workers on y-axis). Use your ogive to estimate:
- the median wage of the workers.
- the lower quartile wage of workers.
- the numbers of workers who earn more than Rs. 625 daily.
Draw an ogive by less than method for the following data:
| No. of rooms: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| No. of houses: | 4 | 9 | 22 | 28 | 24 | 12 | 8 | 6 | 5 | 2 |
The marks scored by 750 students in an examination are given in the form of a frequency distribution table:
| Marks | No. of students |
| 600 - 640 | 16 |
| 640 - 680 | 45 |
| 680 - 720 | 156 |
| 720 - 760 | 284 |
| 760 - 800 | 172 |
| 800 - 840 | 59 |
| 840 - 880 | 18 |
The following table gives the height of trees:
| Height | No. of trees |
| Less than 7 Less than 14 Less than 21 Less than 28 Less than 35 Less than 42 Less than 49 Less than 56 |
26 57 92 134 216 287 341 360 |
Draw 'less than' ogive and 'more than' ogive.
Draw a cumulative frequency curve (ogive) for the following distributions:
| Class Interval | 10 – 19 | 20 – 29 | 30 – 39 | 40 – 49 | 50 – 59 |
| Frequency | 23 | 16 | 15 | 20 | 12 |
Draw an ogive for the following distributions:
| Marks obtained | less than 10 | less than 20 | less than 30 | less than 40 | less than 50 |
| No. of students | 8 | 25 | 38 | 50 | 67 |
Draw an ogive for the following distributions:
| Age in years (less than) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| Cumulative frequency | 0 | 17 | 32 | 37 | 53 | 58 | 65 |
The marks obtained by 100 students of a class in an examination are given below.
| Marks | No. of students |
| 0-5 | 2 |
| 5-10 | 5 |
| 10-15 | 6 |
| 15-20 | 8 |
| 20-25 | 10 |
| 25-30 | 25 |
| 30-35 | 20 |
| 35-40 | 18 |
| 40-45 | 4 |
| 45-50 | 2 |
Draw 'a less than' type cumulative frequency curves (orgive). Hence find median
Using a graph paper, drawn an Ogive for the following distribution which shows a record of the weight in kilograms of 200 students.
| Weight | Frequency |
| 40 - 45 | 5 |
| 45 - 50 | 17 |
| 50 - 55 | 22 |
| 55 - 60 | 45 |
| 60 - 65 | 51 |
| 65 - 70 | 31 |
| 70 - 75 | 20 |
| 75 - 80 | 9 |
Use your ogive to estimate the following:
(i) The percentage of students weighing 55kg or more.
(ii) The weight above which the heaviest 30% of the students fall.
(iii) The number of students who are:
(1) under-weight and
(2) over-weight, if 55·70 kg is considered as standard weight.
Cumulative frequency curve is also called ______.
