Advertisements
Advertisements
Question
The average kinetic energy of molecules in a gas at temperature T is 1.5 kT. Find the temperature at which the average kinetic energy of the molecules of hydrogen equals the binding energy of its atoms. Will hydrogen remain in molecular from at this temperature? Take k = 8.62 × 10−5 eV K−1.
Solution
Average kinetic energy (K) of the molecules in a gas at temperature (T) is given by
K = `3/2 kT`
Here,
k = 8.62 × 10−5 eVK−1
T = Temperature of gas
The binding energy of hydrogen atom is 13.6 eV.
According to the question,
Average kinetic energy of hydrogen molecules = Binding energy of hydrogen atom
∴ 1.5 kT = 13.6
⇒ 1.5 × 8.62 × 10−5 × T = 13.6
`rArr T = (13.6)/(1.5xx8.62xx10^-5)`
No, it is impossible for hydrogen to remain in molecular state at such a high temperature.
APPEARS IN
RELATED QUESTIONS
The first excited energy of a He+ ion is the same as the ground state energy of hydrogen. Is it always true that one of the energies of any hydrogen-like ion will be the same as the ground state energy of a hydrogen atom?
Which wavelengths will be emitted by a sample of atomic hydrogen gas (in ground state) if electrons of energy 12.2 eV collide with the atoms of the gas?
When white radiation is passed through a sample of hydrogen gas at room temperature, absorption lines are observed in Lyman series only. Explain.
In which of the following transitions will the wavelength be minimum?
Which of the following curves may represent the speed of the electron in a hydrogen atom as a function of trincipal quantum number n?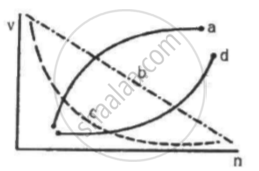
Let An be the area enclosed by the nth orbit in a hydrogen atom. The graph of ln (An/A1) against ln(n)
(a) will pass through the origin
(b) will be a straight line with slope 4
(c) will be a monotonically increasing nonlinear curve
(d) will be a circle
Ionization energy of a hydrogen-like ion A is greater than that of another hydrogen-like ion B. Let r, u, E and L represent the radius of the orbit, speed of the electron, energy of the atom and orbital angular momentum of the electron respectively. In ground state
A hydrogen atom emits ultraviolet radiation of wavelength 102.5 nm. What are the quantum numbers of the states involved in the transition?
Find the maximum Coulomb force that can act on the electron due to the nucleus in a hydrogen atom.
A hydrogen atom in state n = 6 makes two successive transitions and reaches the ground state. In the first transition a photon of 1.13 eV is emitted. (a) Find the energy of the photon emitted in the second transition (b) What is the value of n in the intermediate state?
What is the energy of a hydrogen atom in the first excited state if the potential energy is taken to be zero in the ground state?
A gas of hydrogen-like ions is prepared in a particular excited state A. It emits photons having wavelength equal to the wavelength of the first line of the Lyman series together with photons of five other wavelengths. Identify the gas and find the principal quantum number of the state A.
Find the temperature at which the average thermal kinetic energy is equal to the energy needed to take a hydrogen atom from its ground state to n = 3 state. Hydrogen can now emit red light of wavelength 653.1 nm. Because of Maxwellian distribution of speeds, a hydrogen sample emits red light at temperatures much lower than that obtained from this problem. Assume that hydrogen molecules dissociate into atoms.
Electrons are emitted from an electron gun at almost zero velocity and are accelerated by an electric field E through a distance of 1.0 m. The electrons are now scattered by an atomic hydrogen sample in ground state. What should be the minimum value of E so that red light of wavelength 656.3 nm may be emitted by the hydrogen?
Consider an excited hydrogen atom in state n moving with a velocity υ(ν<<c). It emits a photon in the direction of its motion and changes its state to a lower state m. Apply momentum and energy conservation principles to calculate the frequency ν of the emitted radiation. Compare this with the frequency ν0 emitted if the atom were at rest.
The Balmer series for the H-atom can be observed ______.
- if we measure the frequencies of light emitted when an excited atom falls to the ground state.
- if we measure the frequencies of light emitted due to transitions between excited states and the first excited state.
- in any transition in a H-atom.
- as a sequence of frequencies with the higher frequencies getting closely packed.
Let En = `(-1)/(8ε_0^2) (me^4)/(n^2h^2)` be the energy of the nth level of H-atom. If all the H-atoms are in the ground state and radiation of frequency (E2 - E1)/h falls on it ______.
- it will not be absorbed at all.
- some of atoms will move to the first excited state.
- all atoms will be excited to the n = 2 state.
- no atoms will make a transition to the n = 3 state.
Positronium is just like a H-atom with the proton replaced by the positively charged anti-particle of the electron (called the positron which is as massive as the electron). What would be the ground state energy of positronium?
