Advertisements
Advertisements
Question
The graph of 3x + 2y = 6 meets the x=axis at point P and the y-axis at point Q. Use the graphical method to find the co-ordinates of points P and Q.
Solution
To draw the graph of 3x + 2y = 6 follows the steps:
First, prepare a table as below:
| X | - 2 | 0 | 2 |
| Y | 6 | 3 | 0 |
Now sketch the graph as shown:
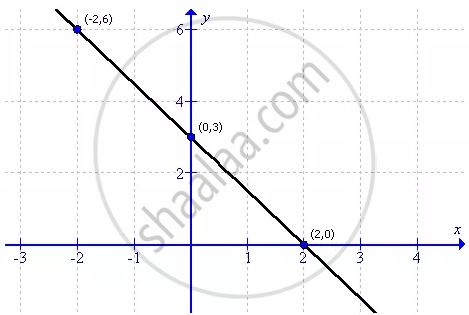
From the graph it can verify that the line intersects the x-axis at (2,0) and y at (0,3), therefore the coordinates of P(x-axis) and Q(y-axis) are (2,0) and (0,3) respectively.
APPEARS IN
RELATED QUESTIONS
Draw the graphs of the following equations on the same system of co-ordinates. Write the co-ordinates of their points of intersection.
x + 4 = 0, y - 1 = 0, 2x + 3 = 0, 3y - 15 = 0
Draw the graph of the equation given below.
3x - y = 0
Draw the graph for the linear equation given below:
y = 3x
Draw the graph for the linear equation given below:
y = - x
Draw the graph for the linear equation given below:
y = `4x - (5)/(2)`
On the same graph paper, plot the graphs of y = 2x - 1, y = 2x and y = 2x + 1 from x = - 2 to x = 4. Are the graphs (lines) drawn parallel to each other?
Draw a graph of each of the following equations: 2(x - 5) = `(3)/(4)(y - 1)`
Draw a graph for each of the following equations and find the coordinates of the points where the line drawn meets the x-axis and y-axis: 2x + 3y = 12
Draw the graph of the lines represented by the equations 3x - 2y = 4 and x + y = 3 on the same graph. Find the coordinates of the point where they intersect. State, whether the lines are perpendicular to each other.
Draw the graph of the lines represented by the equations 2x - y = 8 and 4x + 3y = 6 on the same graph. Find the co-ordinates of the point where they intersect.
