Advertisements
Advertisements
Question
The hypotenuse of a right=-angled triangle is 20 meters. If the difference between the lengths of the other sides be 4 meters, find the other sides
Solution
Let one side of the right-angled triangle be x m and the other side be `(x+4)m` On applying Pythagoras theorem, we have:
`20^2=(x+4)^2+x^2`
⇒` 400x^2+8x+16+x^2`
⇒ `2x^2+8x-384=0`
⇒`x^2+4x-192=0`
⇒`x^2+16x-12x-192=0`
⇒ `x^2(x+16) -12(x+16)=0`
⇒`(x+16) (x-12)=0`
⇒` x=-16 or x=12`
The value of x cannot be negative.
Therefore, the base is 12 m and the other side is `{(12+4)=16m}`
APPEARS IN
RELATED QUESTIONS
Solve for x:
`16/x-1=15/(x+1);x!=0,-1`
Find the roots of the quadratic equations 2x2 + x + 4 = 0 by applying the quadratic formula.
Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, find the sides of the two squares.
`5x^2-6x-2=0`
Fill in the gaps and complete.
If α, β are roots of quadratic equation,
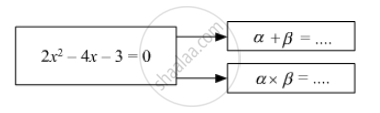
Find the value of discriminant.
2y2 – 5y + 10 = 0
Determine the nature of roots of the following quadratic equation.
x2 – 4x + 4 = 0
α, β are roots of y2 – 2y –7 = 0 find,
α3 + β3
Find two consecutive odd positive integers, sum of whose squares is 970.
In a flight of 600 km, an aircraft was slowed due to bad weather. Its average speed for the trip was reduced by 200 km/hr and the time of the flight increased by 30 minutes. Find the scheduled duration of the flight.
