Advertisements
Advertisements
Question
The marks obtained by 100 students of a class in an examination are given below:
| Marks | Number of students |
| 0 – 5 | 2 |
| 5 – 10 | 5 |
| 10 – 15 | 6 |
| 15 – 20 | 8 |
| 20 – 25 | 10 |
| 25 – 30 | 25 |
| 30 – 35 | 20 |
| 35 – 40 | 18 |
| 40 – 45 | 4 |
| 45 – 50 | 2 |
Draw cumulative frequency curves by using (i) ‘less than’ series and (ii) ‘more than’ series.Hence, find the median.
Solution
(i) From the given table, we may prepare the ‘less than’ frequency table as shown below:
| Marks | Number of students |
| Less than 5 | 2 |
| Less than 10 | 7 |
| Less than 15 | 13 |
| Less than 20 | 21 |
| Less than 25 | 31 |
| Less than 30 | 56 |
| Less than 35 | 76 |
| Less than 40 | 94 |
| Less than 45 | 98 |
| Less than 50 | 100 |
We plot the points A(5, 2), B(10, 7), C(15, 13), D(20, 21), E(25, 31), F(30, 56), G(35, 76) and H(40, 94), I(45, 98) and J(50, 100).
Join AB, BC, CD, DE, EF, FG, GH, HI, IJ and JA with a free hand to get the curve representing the ‘less than type’ series.
(ii) More than series:
| Marks | Number of students |
| More than 0 | 100 |
| More than 5 | 98 |
| More than 10 | 93 |
| More than 15 | 87 |
| More than 20 | 79 |
| More than 25 | 69 |
| More than 30 | 44 |
| More than 35 | 24 |
| More than 40 | 6 |
| More than 45 | 2 |
Now, on the same graph paper, we plot the points (0, 100), (5, 98), (10, 94), (15, 76), (20, 56), (25, 31), (30, 21), (35, 13), (40, 6) and (45, 2). Join with a free hand to get the ‘more than type’ series.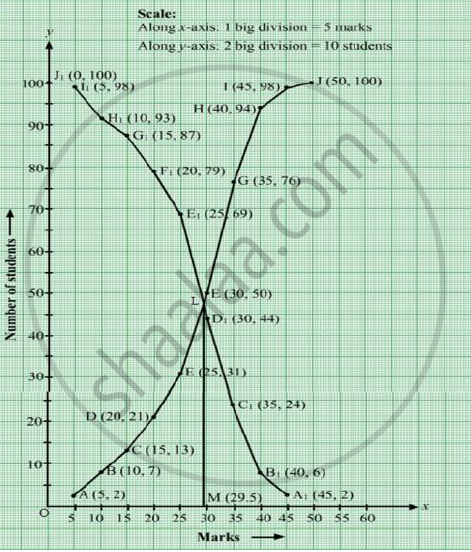
The two curves intersect at point L. Draw LM ⊥ OX cutting the x-axis at M.
Clearly, M = 29.5
Hence, Median = 29.5
APPEARS IN
RELATED QUESTIONS
The monthly profits (in Rs.) of 100 shops are distributed as follows:
| Profits per shop: | 0 - 50 | 50 - 100 | 100 - 150 | 150 - 200 | 200 - 250 | 250 - 300 |
| No. of shops: | 12 | 18 | 27 | 20 | 17 | 6 |
Draw the frequency polygon for it.
From the following data, draw the two types of cumulative frequency curves and determine the median:
| Marks | Frequency |
| 140 – 144 | 3 |
| 144 – 148 | 9 |
| 148 – 152 | 24 |
| 152 – 156 | 31 |
| 156 – 160 | 42 |
| 160 – 164 | 64 |
| 164 – 168 | 75 |
| 168 – 172 | 82 |
| 172 – 176 | 86 |
| 176 – 180 | 34 |
What is the lower limit of the modal class of the following frequency distribution?
| Age (in years) | 0 - 10 | 10- 20 | 20 -30 | 30 – 40 | 40 –50 | 50 – 60 |
| Number of patients | 16 | 13 | 6 | 11 | 27 | 18 |
The following is the cumulative frequency distribution ( of less than type ) of 1000 persons each of age 20 years and above . Determine the mean age .
| Age below (in years): | 30 | 40 | 50 | 60 | 70 | 80 |
| Number of persons : | 100 | 220 | 350 | 750 | 950 | 1000 |
In the formula `barx=a+h((sumf_iu_i)/(sumf_i))`, for finding the mean of grouped frequency distribution ui = ______.
If the median of the following frequency distribution is 32.5. Find the values of f1 and f2.
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | Total |
| Frequency | f1 | 5 | 9 | 12 | f2 | 3 | 2 | 40 |
For one term, absentee record of students is given below. If mean is 15.5, then the missing frequencies x and y are.
| Number of days | 0 - 5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 - 30 | 30 - 35 | 35 - 40 | TOTAL |
| Total Number of students | 15 | 16 | x | 8 | y | 8 | 6 | 4 | 70 |
Look at the following table below.
| Class interval | Classmark |
| 0 - 5 | A |
| 5 - 10 | B |
| 10 - 15 | 12.5 |
| 15 - 20 | 17.5 |
The value of A and B respectively are?
Form the frequency distribution table from the following data:
| Marks (out of 90) | Number of candidates |
| More than or equal to 80 | 4 |
| More than or equal to 70 | 6 |
| More than or equal to 60 | 11 |
| More than or equal to 50 | 17 |
| More than or equal to 40 | 23 |
| More than or equal to 30 | 27 |
| More than or equal to 20 | 30 |
| More than or equal to 10 | 32 |
| More than or equal to 0 | 34 |
Given below is a cumulative frequency distribution showing the marks secured by 50 students of a class:
| Marks | Below 20 | Below 40 | Below 60 | Below 80 | Below 100 |
| Number of students | 17 | 22 | 29 | 37 | 50 |
Form the frequency distribution table for the data.
