Advertisements
Advertisements
प्रश्न
The marks obtained by 100 students of a class in an examination are given below:
| Marks | Number of students |
| 0 – 5 | 2 |
| 5 – 10 | 5 |
| 10 – 15 | 6 |
| 15 – 20 | 8 |
| 20 – 25 | 10 |
| 25 – 30 | 25 |
| 30 – 35 | 20 |
| 35 – 40 | 18 |
| 40 – 45 | 4 |
| 45 – 50 | 2 |
Draw cumulative frequency curves by using (i) ‘less than’ series and (ii) ‘more than’ series.Hence, find the median.
उत्तर
(i) From the given table, we may prepare the ‘less than’ frequency table as shown below:
| Marks | Number of students |
| Less than 5 | 2 |
| Less than 10 | 7 |
| Less than 15 | 13 |
| Less than 20 | 21 |
| Less than 25 | 31 |
| Less than 30 | 56 |
| Less than 35 | 76 |
| Less than 40 | 94 |
| Less than 45 | 98 |
| Less than 50 | 100 |
We plot the points A(5, 2), B(10, 7), C(15, 13), D(20, 21), E(25, 31), F(30, 56), G(35, 76) and H(40, 94), I(45, 98) and J(50, 100).
Join AB, BC, CD, DE, EF, FG, GH, HI, IJ and JA with a free hand to get the curve representing the ‘less than type’ series.
(ii) More than series:
| Marks | Number of students |
| More than 0 | 100 |
| More than 5 | 98 |
| More than 10 | 93 |
| More than 15 | 87 |
| More than 20 | 79 |
| More than 25 | 69 |
| More than 30 | 44 |
| More than 35 | 24 |
| More than 40 | 6 |
| More than 45 | 2 |
Now, on the same graph paper, we plot the points (0, 100), (5, 98), (10, 94), (15, 76), (20, 56), (25, 31), (30, 21), (35, 13), (40, 6) and (45, 2). Join with a free hand to get the ‘more than type’ series.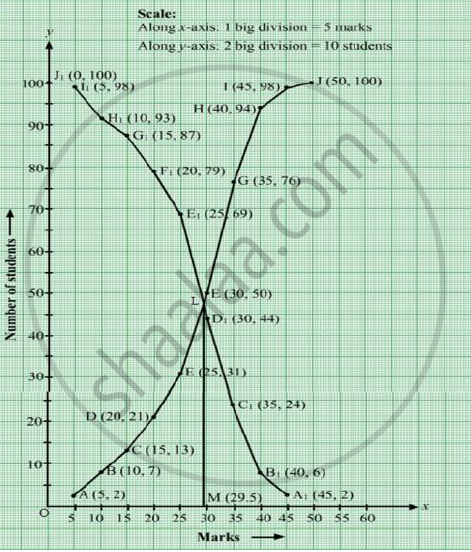
The two curves intersect at point L. Draw LM ⊥ OX cutting the x-axis at M.
Clearly, M = 29.5
Hence, Median = 29.5
APPEARS IN
संबंधित प्रश्न
During the medical check-up of 35 students of a class, their weights were recorded as follows:
| Weight (in kg | Number of students |
| Less than 38 | 0 |
| Less than 40 | 3 |
| Less than 42 | 5 |
| Less than 44 | 9 |
| Less than 46 | 14 |
| Less than 48 | 28 |
| Less than 50 | 32 |
| Less than 52 | 35 |
Draw a less than type ogive for the given data. Hence obtain the median weight from the graph verify the result by using the formula.
Find the median of the following data by making a ‘less than ogive’.
| Marks | 0 - 10 | 10-20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 | 70 - 80 | 80-90 | 90-100 |
| Number of Students | 5 | 3 | 4 | 3 | 3 | 4 | 7 | 9 | 7 | 8 |
The heights of 50 girls of Class X of a school are recorded as follows:
| Height (in cm) | 135 - 140 | 140 – 145 | 145 – 150 | 150 – 155 | 155 – 160 | 160 – 165 |
| No of Students | 5 | 8 | 9 | 12 | 14 | 2 |
Draw a ‘more than type’ ogive for the above data.
What is the lower limit of the modal class of the following frequency distribution?
| Age (in years) | 0 - 10 | 10- 20 | 20 -30 | 30 – 40 | 40 –50 | 50 – 60 |
| Number of patients | 16 | 13 | 6 | 11 | 27 | 18 |
What is the cumulative frequency of the modal class of the following distribution?
| Class | 3 – 6 | 6 – 9 | 9 – 12 | 12 – 15 | 15 – 18 | 18 – 21 | 21 – 24 |
|
Frequency |
7 | 13 | 10 | 23 | 54 | 21 | 16 |
Calculate the missing frequency form the following distribution, it being given that the median of the distribution is 24
| Age (in years) | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Number of persons |
5 | 25 | ? | 18 | 7 |
Write the modal class for the following frequency distribution:
| Class-interval: | 10−15 | 15−20 | 20−25 | 25−30 | 30−35 | 35−40 |
| Frequency: | 30 | 35 | 75 | 40 | 30 | 15 |
In the formula `barx=a+h((sumf_iu_i)/(sumf_i))`, for finding the mean of grouped frequency distribution ui = ______.
Consider the following frequency distributions
| Class | 65 - 85 | 85 - 105 | 105 - 125 | 125 - 145 | 145 - 165 | 165 - 185 | 185-205 |
| Frequency | 4 | 5 | 13 | 20 | 14 | 7 | 4 |
The difference of the upper limit of the median class and the lower limit of the modal class is?
The arithmetic mean of the following frequency distribution is 53. Find the value of k.
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Frequency | 12 | 15 | 32 | k | 13 |
