Advertisements
Advertisements
प्रश्न
From the following frequency, prepare the ‘more than’ ogive.
| Score | Number of candidates |
| 400 – 450 | 20 |
| 450 – 500 | 35 |
| 500 – 550 | 40 |
| 550 – 600 | 32 |
| 600 – 650 | 24 |
| 650 – 700 | 27 |
| 700 – 750 | 18 |
| 750 – 800 | 34 |
| Total | 230 |
Also, find the median.
उत्तर
From the given table, we may prepare than ‘more than’ frequency table as shown below:
| Score | Number of candidates |
| More than 750 | 34 |
| More than 700 | 52 |
| More than 650 | 79 |
| More than 600 | 103 |
| More than 550 | 135 |
| More than 500 | 175 |
| More than 450 | 210 |
| More than 400 | 230 |
We plot the points A(750, 34), B(700,52),
C(650, 79), D(600, 103), E(550, 135), F(500, 175),
G(450, 210) and H(400, 230).
Join AB, BC, CD, DE, EF, FG, GH and HA with
a free hand to get the curve representing the
‘more than type’ series.
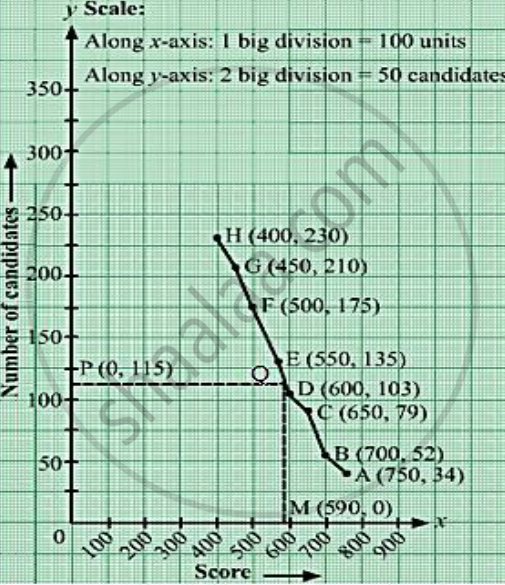
Here, N = 230
⇒ `N/2 = 115`
From P (0, 115), draw PQ meeting the curve at Q. Draw QM meeting at M.
Clearly, OM = 590 units
Hence, median = 590 units.
APPEARS IN
संबंधित प्रश्न
The following distribution gives the daily income of 50 workers of a factory.
| Daily income (in Rs | 100 − 120 | 120 − 140 | 140 − 160 | 160 − 180 | 180 − 200 |
| Number of workers | 12 | 14 | 8 | 6 | 10 |
Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
The following table gives production yield per hectare of wheat of 100 farms of a village.
| Production yield (in kg/ha) | 50 − 55 | 55 − 60 | 60 − 65 | 65 − 70 | 70 − 75 | 75 − 80 |
| Number of farms | 2 | 8 | 12 | 24 | 38 | 16 |
Change the distribution to a more than type distribution and draw ogive.
The given distribution shows the number of wickets taken by the bowlers in one-day international cricket matches:
| Number of Wickets | Less than 15 | Less than 30 | Less than 45 | Less than 60 | Less than 75 | Less than 90 | Less than 105 | Less than 120 |
| Number of bowlers | 2 | 5 | 9 | 17 | 39 | 54 | 70 | 80 |
Draw a ‘less than type’ ogive from the above data. Find the median.
Draw a ‘more than’ ogive for the data given below which gives the marks of 100 students.
| Marks | 0 – 10 | 10 – 20 | 20 – 30 | 30 - 40 | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 |
| No of Students | 4 | 6 | 10 | 10 | 25 | 22 | 18 | 5 |
From the following data, draw the two types of cumulative frequency curves and determine the median:
| Marks | Frequency |
| 140 – 144 | 3 |
| 144 – 148 | 9 |
| 148 – 152 | 24 |
| 152 – 156 | 31 |
| 156 – 160 | 42 |
| 160 – 164 | 64 |
| 164 – 168 | 75 |
| 168 – 172 | 82 |
| 172 – 176 | 86 |
| 176 – 180 | 34 |
The following are the ages of 300 patients getting medical treatment in a hospital on a particular day:
| Age (in years) | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 -70 |
| Number of patients | 6 | 42 | 55 | 70 | 53 | 20 |
Form a ‘less than type’ cumulative frequency distribution.
Consider the following frequency distribution :
| Class: | 0-5 | 6-11 | 12-17 | 18-23 | 24-29 |
| Frequency: | 13 | 10 | 15 | 8 | 11 |
The upper limit of the median class is
The marks obtained by 100 students of a class in an examination are given below.
| Mark | No. of Student |
| 0 - 5 | 2 |
| 5 - 10 | 5 |
| 10 - 15 | 6 |
| 15 - 20 | 8 |
| 20 - 25 | 10 |
| 25 - 30 | 25 |
| 30 - 35 | 20 |
| 35 - 40 | 18 |
| 40 - 45 | 4 |
| 45 - 50 | 2 |
Draw 'a less than' type cumulative frequency curves (ogive). Hence find the median.
If the sum of all the frequencies is 24, then the value of z is:
| Variable (x) | 1 | 2 | 3 | 4 | 5 |
| Frequency | z | 5 | 6 | 1 | 2 |
Given below is a cumulative frequency distribution showing the marks secured by 50 students of a class:
| Marks | Below 20 | Below 40 | Below 60 | Below 80 | Below 100 |
| Number of students | 17 | 22 | 29 | 37 | 50 |
Form the frequency distribution table for the data.
