Advertisements
Advertisements
प्रश्न
The given distribution shows the number of wickets taken by the bowlers in one-day international cricket matches:
| Number of Wickets | Less than 15 | Less than 30 | Less than 45 | Less than 60 | Less than 75 | Less than 90 | Less than 105 | Less than 120 |
| Number of bowlers | 2 | 5 | 9 | 17 | 39 | 54 | 70 | 80 |
Draw a ‘less than type’ ogive from the above data. Find the median.
उत्तर
Taking upper class limits of class intervals on x-axis and their respective frequencies on y-axis, its ogive can be drawn as follows:
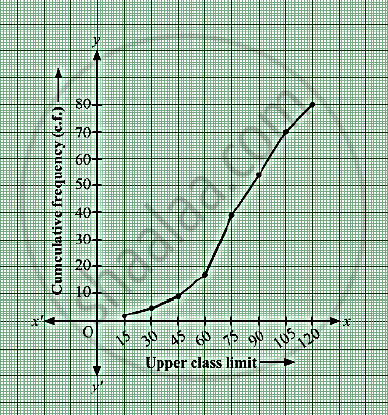
Here, N = 80 ⇒` N/2` = 40.
Mark the point A whose ordinate is 40 and
its x-coordinate is 76.
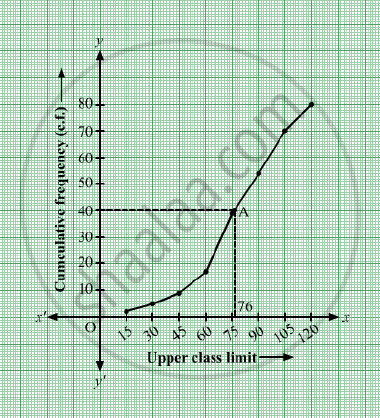
Thus, median of the data is 76.
APPEARS IN
संबंधित प्रश्न
The following distribution gives the daily income of 50 workers of a factory.
| Daily income (in Rs | 100 − 120 | 120 − 140 | 140 − 160 | 160 − 180 | 180 − 200 |
| Number of workers | 12 | 14 | 8 | 6 | 10 |
Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
Find the median of the following data by making a ‘less than ogive’.
| Marks | 0 - 10 | 10-20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 | 70 - 80 | 80-90 | 90-100 |
| Number of Students | 5 | 3 | 4 | 3 | 3 | 4 | 7 | 9 | 7 | 8 |
From the following frequency, prepare the ‘more than’ ogive.
| Score | Number of candidates |
| 400 – 450 | 20 |
| 450 – 500 | 35 |
| 500 – 550 | 40 |
| 550 – 600 | 32 |
| 600 – 650 | 24 |
| 650 – 700 | 27 |
| 700 – 750 | 18 |
| 750 – 800 | 34 |
| Total | 230 |
Also, find the median.
Write the median class for the following frequency distribution:
| Class-interval: | 0−10 | 10−20 | 20−30 | 30−40 | 40−50 | 50−60 | 60−70 | 70−80 |
| Frequency: | 5 | 8 | 7 | 12 | 28 | 20 | 10 | 10 |
For a frequency distribution, mean, median and mode are connected by the relation
The median of a given frequency distribution is found graphically with the help of
If \[u_i = \frac{x_i - 25}{10}, \Sigma f_i u_i = 20, \Sigma f_i = 100, \text { then }\]`overlineX`
If the median of the following frequency distribution is 32.5. Find the values of f1 and f2.
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | Total |
| Frequency | f1 | 5 | 9 | 12 | f2 | 3 | 2 | 40 |
Consider the following distribution:
| Marks obtained | Number of students |
| More than or equal to 0 | 63 |
| More than or equal to 10 | 58 |
| More than or equal to 20 | 55 |
| More than or equal to 30 | 51 |
| More than or equal to 40 | 48 |
| More than or equal to 50 | 42 |
The frequency of the class 30 – 40 is:
Look at the following table below.
| Class interval | Classmark |
| 0 - 5 | A |
| 5 - 10 | B |
| 10 - 15 | 12.5 |
| 15 - 20 | 17.5 |
The value of A and B respectively are?
