Advertisements
Advertisements
Question
The marks scored by the students in social test out of 20 marks are as follows: 12, 10, 8, 18, 14, 16. Find the mean and median?
Solution
Arranging the given data in ascending order: 8, 10, 12, 14, 16, 18
Mean = `"Sum of all observations"/"Number of observations"`
= `(8 + 10 + 12 + 14 + 16 + 18)/6`
= `78/6`
Mean = 13
There are n = 6 observations, which is even
∴ Median = `1/2{("n"/2)^"th" "term" + ("n"/2 + 1)^"th" "term"}`
= `1/2{(6/2)^"th" "term" + (6/2 + 1)^"th" "term"}`
= `1/2{3^"th" "term" + 4^"th" "term"}`
= `1/2{8 + 18}`
= `1/2(26)`
= 13
APPEARS IN
RELATED QUESTIONS
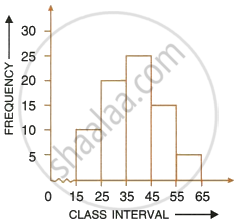
Using the information given in the adjoining histogram, calculate the mean.
Find the mode of following data, using a histogram:
| Class | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Frequency | 5 | 12 | 20 | 9 | 4 |
The monthly income of a group of 320 employees in a company is given below:
| Monthly income (thousands) | No. of employees |
| 6-7 | 20 |
| 7-8 | 45 |
| 8-9 | 65 |
| 9-10 | 95 |
| 10-11 | 60 |
| 11-12 | 30 |
| 12-13 | 5 |
Draw an ogive of the distribution on a graph paper taking 2 cm = Rs. 1000 on one axis and 2 cm = 50 employees on the other axis. From the graph detemine:
- the median wage.
- number of employee whose income is below Rs. 8,500.
- If salary of a senior employee is above Rs. 11,500, find the number of senior employee in the company.
- the upper quartile.
The mean of the following frequency distribution is 25.8 and the sum of all the frequencies is 50. Find x and y.
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequency | 7 | x | 15 | y | 10 |
Find the mean of the following frequency distribution by the step deviation method :
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 | 100-120 | 120-140 |
| Frequency | 12 | 24 | 52 | 88 | 66 | 42 | 16 |
Find the median of:
63, 17, 50, 9, 25, 43, 21, 50, 14 and 34
Find the mean of first six natural numbers.
Find the mean of: first five odd natural numbers
Find the median of 21, 21, 22, 23, 23, 24, 24, 24, 24, 25 and 25
Find the mean and the median of: 1.2, 1.9, 2.2, 2.6 and 2.9
