Advertisements
Advertisements
Question
The points P (4, 1) and Q (–2, 4) are reflected in line y = 3. Find the co-ordinates of P’, the image of P and Q’, the image of Q.
Solution
Co-ordinates of P and Q are (4, 1) and (–2, 4) respectively.
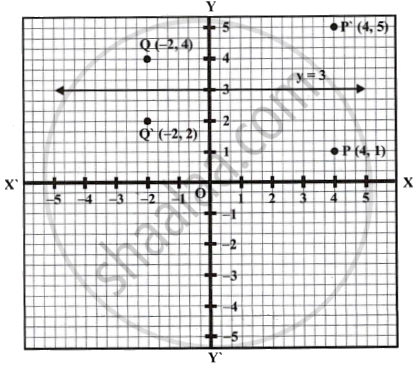
∴ The co-ordinates of image of P which is P' are (4, 5) reflection in the line y = 3 and co-ordinates of image of Q when is Q' are (–2, 2) reflection is the line y = 3 as shown in the graph.
APPEARS IN
RELATED QUESTIONS
Attempt this question on graph paper.
- Plot A (3, 2) and B (5, 4) on graph paper. Take 2 cm = 1 unit on both the axes.
- Reflect A and B in the x-axis to A’ and B’ respectively. Plot these points also on the same graph paper.
- Write down:
- the geometrical name of the figure ABB’A’;
- the measure of angle ABB’;
- the image of A” of A, when A is reflected in the origin.
- the single transformation that maps A’ to A”.
- Point P (a, b) is reflected in the x-axis to P’ (5, –2). Write down the values of a and b.
- P” is the image of P when reflected in the y-axis. Write down the co-ordinates of P”.
- Name a single transformation that maps P’ to P”.
The point (–2, 0) on reflection in a line is mapped to (2, 0) and the point (5, –6) on reflection in the same line is mapped to (–5, –6).
- State the name of the mirror line and write its equation.
- State the co-ordinates of the image of (–8, –5) in the mirror line.
A point P (–2, 3) is reflected in line x = 2 to point P’. Find the co-ordinates of P’.
- Plot the points A (3, 5) and B (–2, –4). Use 1 cm = 1 unit on both the axes.
- A’ is the image of A when reflected in the x-axis. Write down the co-ordinates of A’ and plot it on the graph paper.
- B’ is the image of B when reflected in the y-axis, followed by reflection in the origin. Write down the co-ordinates of B’ and plot it on the graph paper.
- Write down the geometrical name of the figure AA’BB’.
- Name the invariant points under reflection in the x-axis.
The point P (5, 3) was reflected in the origin to get the image P’.
- Write down the co-ordinates of P’.
- If M is the foot of the perpendicular from P to the x-axis, find the co-ordinates of M.
- If N is the foot of the perpendicular from P’ to the x-axis, find the co-ordinates of N.
- Name the figure PMP’N.
- Find the area of the figure PMP’N.
The point P (3, 4) is reflected to P’ in the x-axis; and O’ is the image of O (the origin) when reflected in the line PP’. Write:
- the co-ordinates of P’ and O’.
- the length of the segments PP’ and OO’.
- the perimeter of the quadrilateral POP’O’.
- the geometrical name of the figure POP’O’.
A (1, 1), B (5, 1), C (4, 2) and D (2, 2) are vertices of a quadrilateral. Name the quadrilateral ABCD. A, B, C, and D are reflected in the origin on to A’, B’, C’ and D’ respectively. Locate A’, B’, C’ and D’ on the graph sheet and write their co-ordinates. Are D, A, A’ and D’ collinear?
The triangle ABC, where A is (2, 6), B is (–3, 5) and C is (4, 7), is reflected in the y-axis to triangle A'B'C'. Triangle A'B'C' is then reflected in the origin to triangle A"B"C".
- Write down the co-ordinates of A", B" and C".
- Write down a single transformation that maps triangle ABC onto triangle A"B"C".
Points (3, 0) and (-1, 0) are invarient points under reflection in the line L1; point (0, -3) and (0, 1) are invarient points on reflection in line L2.
(i) Write the equation of the line L1 and L2.
(ii) Write down the images of points P(3, 4) and Q(-5, -2) on reflection in L1. Name the images as P' and Q' respectively.
(iii) Write down the images of P and Q on reflection in L2. Name the image as P'' and Q'' respectively.
