Advertisements
Advertisements
Question
The radius of planet A is half the radius of planet B. If the mass of A is MA, what must be the mass of B so that the value of g on B is half that of its value on A?
Solution 1
The acceleration due to gravity of a planet is given as
\[\text{g} = \frac{\text{GM}}{\text{r}^2}\]
For planet A:
For planet B:
\[\text{g}_{B} = \frac{\text{GM}_\text{B}}{\text{r}_\text{B}^2}\]
\[\text{g}_\text{B} = \frac{1}{2} \text{g}_\text{A}\] ...(Given) or,
\[\frac{\text{GM}_\text{B}}{\text{r}_\text{B}^2} = \frac{\text{G M}_\text{A}}{2 \text{r}_\text{A}^2}\]
\[\Rightarrow \text{M}_\text{B} = \frac{\text{M}_\text{A} \text{r}_\text{B}^2}{2 \text{r}_\text{A}^2}\]
\[\Rightarrow \text{M}_\text{B} = \frac{\text{M}_\text{A} \text{r}_\text{B}^2}{2(\frac{1}{2} \text{r}_\text{B})^2} = 2 \text{M}_\text{A}\]
Solution 2
radius of planet ‘A’ = RA, radius of planet ‘B’ = RB
Mass of planet ‘A’ = MA, mass of planet ‘B’ = MB = ?
From given...
`"R"_"A" = ("R"_"B")/2; "g"_"B" = 1/2 "g"_"A"`
`"g" = ("GM")/("R"^2);`
`∴ "g"_"A" = ("GM"_"A")/("R"_"A"^2)`;
`∴ "g"_"B" = ("GM"_"B")/("R"_"B"^2)`
`("GM"_"B")/("R"_"B"^2)`
`("M"_"B")/("R"_"B"^2) = 1/2(("GM"_"A")/(("RB"/2)^2))`
`("M"_"B")/("R"_"B"^2) = 1/2 (4("GM"_"A")/(("R"_"B")^2))`
`"M"_"B" = 2 "M"_"A"`
APPEARS IN
RELATED QUESTIONS
State whether the following statement is true or false :
The value of G on the moon is about one-sixth `(1/6)`of the value of G on the earth.
Why does the velocity of a stone thrown vertically upwards decreases?
The value of g is highest at the equator.
The value of G varies from place to place.
As we go above the earth's surface, value of g increases.
The mass of the moon is `1/81` of the mass of the earth. Its diameter is `1/3.7` of that of the earth. If acceleration due to gravity on the surface of the earth is 9.8 m/s2, then the acceleration due to gravity on the surface of the moon.
The mass of a body on the surface of the earth is 10 kg. The mass of the same body on the surface on the moon is `"g"_"m" = 1/6 "g"_"e"`, where gm, ge acceleration due to gravity on the surface of the moon and the earth respectively.
The acceleration due to gravity on a planet is 1.96 m/s2. If it is safe to jump from a height of 3 m on tbe earth, the corresponding height on the planet will be ____________.
The acceleration due to gravity on moon is `(1/6)^"th"` times the acceleration due to gravity on earth. If the ratio of the density of earth 'ρe' to the density of moon 'ρm' is `5/3`, then the radius of moon 'Rm' in terms of the radius of earth 'Re' is ______.
When the value of acceleration due to gravity 'g' becomes `(g/3)` above the earth's surface at height 'h' then relation between 'h' and 'R' is ______.
R =radius of the earth
A wire AB is carrying steady current 'I1' and is kept on the table. Another wire CD carrying current 'I2' is held parallel and directly above AB at a distance 'r'. When wire CD is left free and it remains suspended at its position, its mass per unit length is (g =acceleration due to gravity) ____________.
In the relation F = `"G M" "m"//"d"^2`, the quantity G
Suppose the gravity of the earth suddenly becomes zero, then in which direction will the moon begin to move if no other celestial body affects it?
Write if the following statement is correct or wrong.
The value of g is the same everywhere on the surface of the earth.
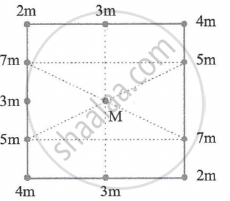
A central particle M is surrounded by a square array of other particles, separated by either distanced or distance d/2 along the perimeter o the square. The magnitude of the gravitational force on the central particle due to the other particles is ______.
A body is thrown from the surface of the earth with velocity 'u' m/s. The maximum height in m above the surface of the earth upto which it will reach is ______.
(R = radius of earth, g = acceleration due to gravity)
A lift of mass 'm' is connected to a rope which is moving upward with maximum acceleration 'a'. For maximum safe stress, the elastic limit of the rope is 'T'. The minimum diameter of the rope is ______.
(g = gravitational acceleration)
If the change in the value of g at the height h above the surface of the earth is the same as at a depth x below it, then ______.
(both x and h being much smaller than the radius of the earth)
