Advertisements
Advertisements
Question
The square of its period of revolution around the sun is directly proportional to the _______ of the mean distance of a planet from the sun.
Options
square
square root
cube
cube root
Solution
The square of its period of revolution around the sun is directly proportional to the cube of the mean distance of a planet from the sun.
APPEARS IN
RELATED QUESTIONS
Let us assume that our galaxy consists of 2.5 × 1011 stars each of one solar mass. How long will a star at a distance of 50,000 ly from the galactic centre take to complete one revolution? Take the diameter of the Milky Way to be 105 ly
A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant (a) linear speed, (b) angular speed, (c) angular momentum, (d) kinetic energy, (e) potential energy, (f) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the Sun.
State Kepler's laws of planetary motion.
In the Following figure shows the elliptical path of a planet about the sun. The two shaded parts have equal area. If t1 and t2 be the time taken by the planet to go from a to b and from c to d respectively,
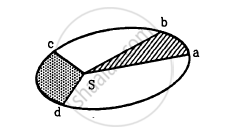
Answer the following question.
State Kepler’s law of the period.
Observe the given figure showing the orbit of a planet moving around the Sun and write the three laws related to it:

The orbit of a planet moving around the Sun
Write the Kepler's laws.
The third law of Kepler is also known as the Law of ______.
State Kepler’s laws.
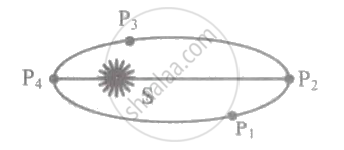
A planet is revolving around the sun in an elliptical orbit as shown in figure. At which point will its K.E. be maximum?
To verify Kepler's third law graphically four students plotted graphs. Student A plotted a graph of T (period of revolution of planets) versus r (average distance of planets from the sun) and found the plot is straight line with slope 1.85. Student B plotted a graph of T2 v/s r3 and found the plot is straight line with slope 1.39 and negative Y-intercept. Student C plotted graph of log T v/s log r and found the plot is straight line with slope 1.5. Student D plotted graph of log T v/s log r and found the plot is straight line with slope 0.67 and with negative X-intercept. The correct graph is of student
If the sun and the planets carried huge amounts of opposite charges ______.
- all three of Kepler’s laws would still be valid.
- only the third law will be valid.
- the second law will not change.
- the first law will still be valid.
Supposing Newton’s law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read F1 = – F2 = `- r_12/r_12^3 GM_0^2 ((m_1m_2)/M_0^2)^n` where M0 is a constant of dimension of mass r12 = r1 – r2 and n is a number. in such a case.
- the acceleration due to gravity on earth will be different for different objects.
- none of the three laws of Kepler will be valid.
- only the third law will become invalid.
- for n negative, an object lighter than water will sink in water.
The centre of mass of an extended body on the surface of the earth and its centre of gravity ______.
- are always at the same point for any size of the body.
- are always at the same point only for spherical bodies.
- can never be at the same point.
- is close to each other for objects, say of sizes less than 100 m.
- both can change if the object is taken deep inside the earth.
Give one example each of central force and non-central force.
A star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be v, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E and angular momentum l. As the radius r of the orbit increases, determine which of the above quantities increase and which ones decrease.
Earth’s orbit is an ellipse with eccentricity 0.0167. Thus, earth’s distance from the sun and speed as it moves around the sun varies from day to day. This means that the length of the solar day is not constant through the year. Assume that earth’s spin axis is normal to its orbital plane and find out the length of the shortest and the longest day. A day should be taken from noon to noon. Does this explain variation of length of the day during the year?
Two planets A and B of equal mass are having their period of revolutions TA and TB such that TA = 2TB. These planets are revolving in the circular orbits of radii rA and rB respectively. Which out of the following would be the correct relationship of their orbits?
