Advertisements
Advertisements
Question
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
Solution
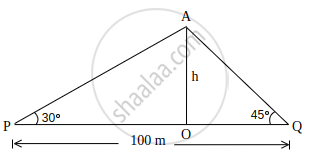
Let OA be the tree of height h m.
In ΔPOA, ∠O = 90°
tan 30° = `("OA")/("OP")`
⇒ `1/sqrt(3) = "h"/("OP")`
⇒ OP = `sqrt(3) "h"` ...(i)
In ΔQOA, ∠O = 90°
tan 45° = `("OA")/("OQ")`
⇒ `1 = "h"/("OQ")`
⇒ OQ = h ...(ii)
Adding equations (i) and (ii), we get
OP + OQ = `sqrt(3) "h" + "h"`
⇒ PQ = `"h"(sqrt(3) + 1)`
⇒ 100 = `"h"(sqrt(3) + 1)`
⇒ h = `100/(sqrt(3) + 1)`
⇒ h = `(100(sqrt(3) - 1))/((sqrt(3) + 1)(sqrt(3) - 1))`
⇒ h = `(100(sqrt(3) - 1))/2`
⇒ h = 50 (1.732 – 1)
⇒ h = 50 × 0.732
⇒ h = 36.6m
Thus, the height of the tree is 36.6 m.
RELATED QUESTIONS
The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is `\frac{AB\sin \alpha \sin \beta }{\sqrt{\sin^{2}\alpha -\sin ^{2}\beta `
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
A ladder of length 6meters makes an angle of 45° with the floor while leaning against one wall of a room. If the fort of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the
distance between two walls of the room.
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34°. Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
The line drawn from the eye of an observer to the point in the object viewed by the observer is known as ____________.
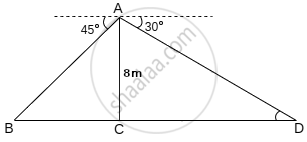
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
