Advertisements
Advertisements
Question
Three cards are drawn successively with replacement from a well-shuffled deck of 52 cards. A random variable X denotes the number of hearts in the three cards drawn. Determine the probability distribution of X.
Solution
Let X denote the number of hearts in a sample of 3 cards drawn from a well-shuffled deck of 52 cards. Then, X can take the values 0, 1, 2 and 3.
Now,
Thus, the probability distribution of X is given by
| X | P(X) |
| 0 |
|
| 1 |
|
| 2 |
|
| 3 |
|
APPEARS IN
RELATED QUESTIONS
State the following are not the probability distributions of a random variable. Give reasons for your answer.
| X | 0 | 1 | 2 | 3 | 4 |
| P(X) | 0.1 | 0.5 | 0.2 | -0.1 | 0.3 |
State the following are not the probability distributions of a random variable. Give reasons for your answer.
| Y | -1 | 0 | 1 |
| P(Y) | 0.6 | 0.1 | 0.2 |
Find the probability distribution of number of heads in two tosses of a coin.
Assume that the chances of the patient having a heart attack are 40%. It is also assumed that a meditation and yoga course reduce the risk of heart attack by 30% and prescription of certain drug reduces its chances by 25%. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga?
A random variable X has the following probability distribution:
| Values of X : | −2 | −1 | 0 | 1 | 2 | 3 |
| P (X) : | 0.1 | k | 0.2 | 2k | 0.3 | k |
Find the value of k.
A random variable X has the following probability distribution:
| Values of X : | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P (X) : | a | 3a | 5a | 7a | 9a | 11a | 13a | 15a | 17a |
Determine:
(i) The value of a
(ii) P (X < 3), P (X ≥ 3), P (0 < X < 5).
The probability distribution function of a random variable X is given by
| xi : | 0 | 1 | 2 |
| pi : | 3c3 | 4c − 10c2 | 5c-1 |
where c > 0 Find: P (1 < X ≤ 2)
Four cards are drawn simultaneously from a well shuffled pack of 52 playing cards. Find the probability distribution of the number of aces.
Five defective mangoes are accidently mixed with 15 good ones. Four mangoes are drawn at random from this lot. Find the probability distribution of the number of defective mangoes.
Two dice are thrown together and the number appearing on them noted. X denotes the sum of the two numbers. Assuming that all the 36 outcomes are equally likely, what is the probability distribution of X?
In roulette, Figure, the wheel has 13 numbers 0, 1, 2, ...., 12 marked on equally spaced slots. A player sets Rs 10 on a given number. He receives Rs 100 from the organiser of the game if the ball comes to rest in this slot; otherwise he gets nothing. If X denotes the player's net gain/loss, find E (X).
An urn contains 5 red and 2 black balls. Two balls are randomly drawn, without replacement. Let X represent the number of black balls drawn. What are the possible values of X ? Is X a random variable ? If yes, then find the mean and variance of X.
Find the mean of the following probability distribution:
| X= xi: | 1 | 2 | 3 |
| P(X= xi) : |
|
|
|
Mark the correct alternative in the following question:
The probability distribution of a discrete random variable X is given below:
| X: | 2 | 3 | 4 | 5 |
| P(X): |
|
|
|
The value of k is .
From a lot of 15 bulbs which include 5 defective, a sample of 4 bulbs is drawn one by one with replacement. Find the probability distribution of number of defective bulbs. Hence, find the mean of the distribution.
A die is tossed twice. A 'success' is getting an even number on a toss. Find the variance of number of successes.
Three cards are drawn successively with replacement from a well shuffled pack of 52 cards. Find the probability distribution of the number of spades. Hence, find the mean of the distribtution.
Verify the following function, which can be regarded as p.m.f. for the given values of X :
| X = x | -1 | 0 | 1 |
| P(x) | -0.2 | 1 | 0.2 |
John and Mathew started a business with their capitals in the ratio 8 : 5. After 8 months, john added 25% of his earlier capital as further investment. At the same time, Mathew withdrew 20% of bis earlier capital. At the end of the year, they earned ₹ 52000 as profit. How should they divide the profit between them?
Verify whether the following function can be regarded as probability mass function (p.m.f.) for the given values of X :
| X | -1 | 0 | 1 |
| P(X = x) | -0.2 | 1 | 0.2 |
The probability that a bomb dropped from an aeroplane will strike a target is
(a) exactly two will strike the target,
(b) at least one will strike the target.
Solve the following :
Identify the random variable as either discrete or continuous in each of the following. Write down the range of it.
20 white rats are available for an experiment. Twelve rats are male. Scientist randomly selects 5 rats number of female rats selected on a specific day
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| x | 0 | 1 | 2 |
| P(x) | 0.4 | 0.4 | 0.2 |
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| x | 0 | 1 | 2 | 3 | 4 |
| P(x) | 0.1 | 0.5 | 0.2 | –0.1 | 0.3 |
In a multiple choice test with three possible answers for each of the five questions, what is the probability of a candidate getting four or more correct answers by random choice?
Defects on plywood sheet occur at random with the average of one defect per 50 Sq.ft. Find the probability that such a sheet has no defect
State whether the following is True or False :
If r.v. X assumes the values 1, 2, 3, ……. 9 with equal probabilities, E(x) = 5.
Solve the following problem :
If a fair coin is tossed 4 times, find the probability that it shows head in the first 2 tosses and tail in last 2 tosses.
Solve the following problem :
The probability that a lamp in the classroom will burn is 0.3. 3 lamps are fitted in the classroom. The classroom is unusable if the number of lamps burning in it is less than 2. Find the probability that the classroom cannot be used on a random occasion.
Solve the following problem :
A computer installation has 3 terminals. The probability that any one terminal requires attention during a week is 0.1, independent of other terminals. Find the probabilities that 0
Solve the following problem :
It is observed that it rains on 10 days out of 30 days. Find the probability that it rains on exactly 3 days of a week.
Let the p.m.f. of a random variable X be P(x) =
Two probability distributions of the discrete random variable X and Y are given below.
| X | 0 | 1 | 2 | 3 |
| P(X) |
| Y | 0 | 1 | 2 | 3 |
| P(Y) |
Prove that E(Y2) = 2E(X).
The random variable X can take only the values 0, 1, 2. Given that P(X = 0) = P(X = 1) = p and that E(X2) = E[X], find the value of p
The probability distribution of a discrete random variable X is given as under:
| X | 1 | 2 | 4 | 2A | 3A | 5A |
| P(X) |
Calculate: Variance of X
A person throws two fair dice. He wins ₹ 15 for throwing a doublet (same numbers on the two dice), wins ₹ 12 when the throw results in the sum of 9, and loses ₹ 6 for any other outcome on the throw. Then the expected gain/loss (in ₹) of the person is ______.
Kiran plays a game of throwing a fair die 3 times but to quit as and when she gets a six. Kiran gets +1 point for a six and –1 for any other number.
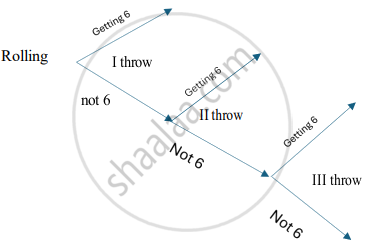
- If X denotes the random variable “points earned” then what are the possible values X can take?
- Find the probability distribution of this random variable X.
- Find the expected value of the points she gets.
