Advertisements
Advertisements
Question
State the following are not the probability distributions of a random variable. Give reasons for your answer.
| Y | -1 | 0 | 1 |
| P(Y) | 0.6 | 0.1 | 0.2 |
Solution
It is known that the sum of all the probabilities in a probability distribution is one.
Sum of the probabilities = 0.6 + 0.1 + 0.2 = 0.9 ≠ 1
Therefore, the given table is not a probability distribution of random variables.
APPEARS IN
RELATED QUESTIONS
A random variable X has the following probability distribution.
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(X) | 0 | k | 2k | 2k | 3k | k2 |
2k2 |
7k2 + k |
Determine
(i) k
(ii) P (X < 3)
(iii) P (X > 6)
(iv) P (0 < X < 3)
Two numbers are selected at random (without replacement) from the first six positive integers. Let X denotes the larger of the two numbers obtained. Find E(X).
Let, X denote the number of colleges where you will apply after your results and P(X = x) denotes your probability of getting admission in x number of colleges. It is given that
where k is a positive constant. Find the value of k. Also find the probability that you will get admission in (i) exactly one college (ii) at most 2 colleges (iii) at least 2 colleges.
Find the probability distribution of the number of heads, when three coins are tossed.
Find the probability distribution of Y in two throws of two dice, where Y represents the number of times a total of 9 appears.
The probability distribution of a random variable X is given below:
| x | 0 | 1 | 2 | 3 |
| P(X) | k |
\[\frac{k}{2}\]
|
\[\frac{k}{4}\]
|
\[\frac{k}{8}\]
|
Find P(X ≤ 2) + P(X > 2) .
Find the mean and standard deviation of each of the following probability distribution :
| xi : | 1 | 2 | 3 | 4 |
| pi : | 0.4 | 0.3 | 0.2 | 0.1 |
Find the mean variance and standard deviation of the following probability distribution
| xi : | a | b |
| pi : | p | q |
A fair coin is tossed four times. Let X denote the number of heads occurring. Find the probability distribution, mean and variance of X.
A die is tossed twice. A 'success' is getting an odd number on a toss. Find the variance of the number of successes.
Write the values of 'a' for which the following distribution of probabilities becomes a probability distribution:
| X= xi: | -2 | -1 | 0 | 1 |
| P(X= xi) : |
\[\frac{1 - a}{4}\]
|
\[\frac{1 + 2a}{4}\]
|
\[\frac{1 - 2a}{4}\]
|
\[\frac{1 + a}{4}\]
|
For what value of k the following distribution is a probability distribution?
| X = xi : | 0 | 1 | 2 | 3 |
| P (X = xi) : | 2k4 | 3k2 − 5k3 | 2k − 3k2 | 3k − 1 |
If the probability distribution of a random variable X is as given below:
Write the value of P (X ≤ 2).
| X = xi : | 1 | 2 | 3 | 4 |
| P (X = xi) : | c | 2c | 4c | 4c |
A random variable X takes the values 0, 1, 2, 3 and its mean is 1.3. If P (X = 3) = 2 P (X = 1) and P (X = 2) = 0.3, then P (X = 0) is
Calculate `"e"_0^circ ,"e"_1^circ , "e"_2^circ` from the following:
| Age x | 0 | 1 | 2 |
| lx | 1000 | 880 | 876 |
| Tx | - | - | 3323 |
If the demand function is D = 150 - p2 - 3p, find marginal revenue, average revenue and elasticity of demand for price p = 3.
Three different aeroplanes are to be assigned to carry three cargo consignments with a view to maximize profit. The profit matrix (in lakhs of ₹) is as follows :
| Aeroplanes | Cargo consignments | ||
| C1 | C2 | C3 | |
| A1 | 1 | 4 | 5 |
| A2 | 2 | 3 | 3 |
| A3 | 3 | 1 | 2 |
How should the cargo consignments be assigned to the aeroplanes to maximize the profit?
If random variable X has probability distribution function.
f(x) = `c/x`, 1 < x < 3, c > 0, find c, E(x) and Var(X)
The expenditure Ec of a person with income I is given by Ec = (0.000035) I2 + (0. 045) I. Find marginal propensity to consume (MPC) and average propensity to consume (APC) when I = 5000.
The p.m.f. of a random variable X is
`"P"(x) = 1/5` , for x = I, 2, 3, 4, 5
= 0 , otherwise.
Find E(X).
The defects on a plywood sheet occur at random with an average of the defect per 50 sq. ft. What Is the probability that such sheet will have-
(a) No defects
(b) At least one defect
[Use e-1 = 0.3678]
A random variable X has the following probability distribution :
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P(X) | C | 2C | 2C | 3C | C2 | 2C2 | 7C2+C |
Find the value of C and also calculate the mean of this distribution.
A sample of 4 bulbs is drawn at random with replacement from a lot of 30 bulbs which includes 6 defective bulbs. Find the probability distribution of the number of defective bulbs.
A pair of dice is thrown 3 times. If getting a doublet is considered a success, find the probability of two successes
The probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5) that fuse after 200 days of use. Find the probability of X ≤ 1
State whether the following is True or False :
If r.v. X assumes the values 1, 2, 3, ……. 9 with equal probabilities, E(x) = 5.
Solve the following problem :
Following is the probability distribution of a r.v.X.
| x | – 3 | – 2 | –1 | 0 | 1 | 2 | 3 |
| P(X = x) | 0.05 | 0.1 | 0.15 | 0.20 | 0.25 | 0.15 | 0.1 |
Find the probability that X is even.
Solve the following problem :
A computer installation has 3 terminals. The probability that any one terminal requires attention during a week is 0.1, independent of other terminals. Find the probabilities that 0
Solve the following problem :
A computer installation has 3 terminals. The probability that any one terminal requires attention during a week is 0.1, independent of other terminals. Find the probabilities that 1 terminal requires attention during a week.
Let the p.m.f. of a random variable X be P(x) = `(3 - x)/10`, for x = −1, 0, 1, 2 = 0, otherwise Then E(x) is ______
Consider the probability distribution of a random variable X:
| X | 0 | 1 | 2 | 3 | 4 |
| P(X) | 0.1 | 0.25 | 0.3 | 0.2 | 0.15 |
Calculate `"V"("X"/2)`
Find the probability distribution of the maximum of the two scores obtained when a die is thrown twice. Determine also the mean of the distribution.
The probability distribution of a discrete random variable X is given as under:
| X | 1 | 2 | 4 | 2A | 3A | 5A |
| P(X) | `1/2` | `1/5` | `3/25` | `1/10` | `1/25` | `1/25` |
Calculate: Variance of X
Box I contains 30 cards numbered 1 to 30 and Box II contains 20 cards numbered 31 to 50. A box is selected at random and a card is drawn from it. The number on the card is found to be a nonprime number. The probability that the card was drawn from Box I is ______.
A person throws two fair dice. He wins ₹ 15 for throwing a doublet (same numbers on the two dice), wins ₹ 12 when the throw results in the sum of 9, and loses ₹ 6 for any other outcome on the throw. Then the expected gain/loss (in ₹) of the person is ______.
Kiran plays a game of throwing a fair die 3 times but to quit as and when she gets a six. Kiran gets +1 point for a six and –1 for any other number.
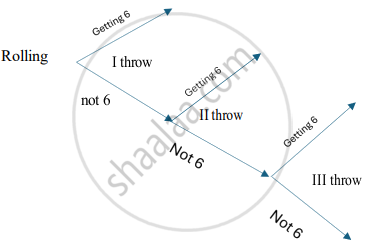
- If X denotes the random variable “points earned” then what are the possible values X can take?
- Find the probability distribution of this random variable X.
- Find the expected value of the points she gets.
