Advertisements
Advertisements
Question
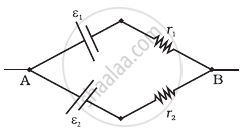
Two batteries of emf ε1 and ε2 (ε2 > ε1) and internal resistances r1 and r2 respectively are connected in parallel as shown in figure.
Options
The equivalent emf εeq of the two cells is between ε1 and ε2, i.e. ε1 < εeq < ε2.
The equivalent emf εeq is smaller than ε1.
The εeq is given by εeq = ε1 + ε2 always.
εeq is independent of internal resistances r1 and r2.
Solution
The equivalent emf εeq of the two cells is between ε1 and ε2, i.e. ε1 < εeq < ε2.
Explanation:
The equivalent emf of this combination is given by
εeq = `(ε_1/r_1 + ε_1/r_2)/((1/r_1 + 1/r_2)) = (ε_1(1/r_1 + (ε_2/ε_1)/r_2))/((1/r_1 + 1/r_2)) = (ε_2((ε_1/ε_2)/r_1 + 1/r_2))/((1/r_1 + 1/r_2))`
As `ε_2/ε_1 > 1`
⇒ `((1/r_1 + (ε_2/r_1)/r_2))/((1/r_1 + 1/r_2)) > 1 or ε_(eq) > ε_1` also `ε_1/ε_2 < 1`
⇒ `(((ε_1/ε_2)/r_1 + 1/r_2))/((1/r_1 + 1/r_2)) < 1 or ε_(eq) < ε_1`
Hence ε1 < εeq < ε2.
APPEARS IN
RELATED QUESTIONS
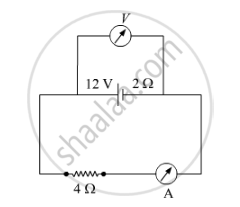
A battery of emf 12 V and internal resistance 2 Ω is connected to a 4 Ω resistor as shown in the figure.
(a) Show that a voltmeter when placed across the cell and across the resistor, in turn, gives the same reading.
(b) To record the voltage and the current in the circuit, why is voltmeter placed in parallel and ammeter in series in the circuit?
Distinguish between emf and terminal voltage of a cell.
A cell of emf 'E' and internal resistance 'r' is connected across a variable resistor 'R'. Plot a graph showing variation of terminal voltage 'V' of the cell versus the current 'I'. Using the plot, show how the emf of the cell and its internal resistance can be determined.
A long straight current carrying wire passes normally through the centre of circular loop. If the current through the wire increases, will there be an induced emf in the loop? Justify.
The equivalent resistance between points. a and f of the network shown in Figure 2 is :
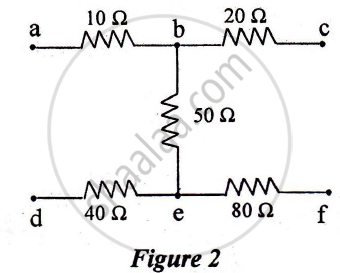
a) 24 Ω
b) 110 Ω
c) 140 Ω
d) 200 Ω
Two cells of emf E1, E2 and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure.

Deduce the expressions for
(1) the equivalent e.m.f of the combination
(2) the equivalent resistance of the combination, and
(3) the potential difference between the point A and B.
A coil of resistance 100 Ω is connected across a battery of emf 6.0 V. Assume that the heat developed in the coil is used to raise its temperature. If the heat capacity of the coil is 4.0 J K−1, how long will it take to raise the temperature of the coil by 15°C?
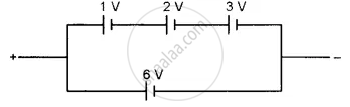
Find the emf of the battery shown in the figure:
A battery of EMF 10V sets up a current of 1A when connected across a resistor of 8Ω. If the resistor is shunted by another 8Ω resistor, what would be the current in the circuit? (in A)
