Advertisements
Advertisements
Question
Two particles X and Y having equal charge, after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of X to that of Y is ______.
Options
(R1/R2)1/2
R1/R2
(R1/R2)2
R1R2.
Solution
Two particles X and Y having equal charge, after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of X to that of Y is (R1/R2)2.
Explanation:
`"R"_1^2/"R"_2^2`
Particles X and Y of respective masses m1 and m2 are carrying charge q describing circular paths with respective radii R1 and R2 such that
`"R"_1 = ("m"_1"v"_1)/"qB"`
`"R"_2 = ("m"_2"v"_2)/"qB"`
Since both the particles are accelerated through the same potential difference, both will have the same kinetic energy.
`therefore 1/2 "m"_1"v"_1^2 = 1/2 "m"_2"v"_2^2`
`because "R"_1 = ("m"_1"v"_1)/"qB" => "v"_1 = ("R"_1"qB")/"m"_1`
And
`because "R"_2 = ("m"_2"v"_2)/"qB" => "v"_2 = ("R"_2"qB")/"m"_2`
`therefore "m"_1 (("R"_1 "qB")/"m"_1)^2 = "m"_2 (("R"_1 "qB")/"m"_1)^2`
`=> "m"_1/"m"_2 = "R"_1^2/"R"_2^2`
APPEARS IN
RELATED QUESTIONS
Write the expression, in a vector form, for the Lorentz magnetic force \[\vec{F}\] due to a charge moving with velocity \[\vec{V}\] in a magnetic field \[\vec{B}\]. What is the direction of the magnetic force?
A proton and an α-particle move perpendicular to a magnetic field. Find the ratio of radii of circular paths described by them when both have (i) equal velocities, and (ii) equal kinetic energy.
An electron moving horizontally with a velocity of 4 ✕ 104 m/s enters a region of uniform magnetic field of 10−5 T acting vertically upward as shown in the figure. Draw its trajectory and find out the time it takes to come out of the region of magnetic
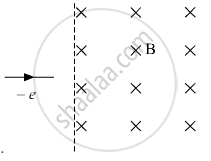
field.
An electric current i enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged particle q, moving along the axis of the circular wire, passes through its centre at speed v. The magnetic force acting on the particle, when it passes through the centre, has a magnitude equal to
An experimenter's diary reads as follows: "A charged particle is projected in a magnetic field of `(7.0 vec i - 3.0 vecj)xx 10^-3 `T. The acceleration of the particle is found to be `(x veci + 7.0 vecj )` The number to the left of i in the last expression was not readable. What can this number be?
A 10 g bullet with a charge of 4.00 μC is fired at a speed of 270 m s−1 in a horizontal direction. A vertical magnetic field of 500 µT exists in the space. Find the deflection of the bullet due to the magnetic field as it travels through 100 m. Make appropriate approximations.
When a proton is released from rest in a room, it starts with an initial acceleration a0towards west. When it is projected towards north with a speed v0, it moves with an initial acceleration 3a0 towards west. Find the electric field and the maximum possible magnetic field in the room.
A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
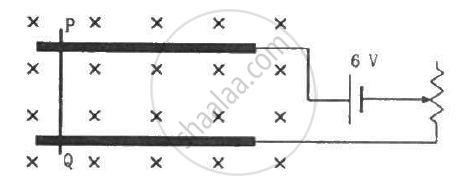
A metal wire PQ of mass 10 g lies at rest on two horizontal metal rails separated by 4.90 cm (figure). A vertically-downward magnetic field of magnitude 0.800 T exists in the space. The resistance of the circuit is slowly decreased and it is found that when the resistance goes below 20.0 Ω, the wire PQ starts sliding on the rails. Find the coefficient of friction.
Protons with kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field, so that it just misses a plane target kept at a distance l in front of the accelerator. Find the magnetic field.
A circular coil of radius 2.0 cm has 500 turns and carries a current of 1.0 A. Its axis makes an angle of 30° with the uniform magnetic field of magnitude 0.40 T that exists in the space. Find the torque acting on the coil.
A narrow beam of singly charged potassium ions of kinetic energy 32 keV is injected into a region of width 1.00 cm with a magnetic field of strength 0.500 T, as shown in the figure. The ions are collected at a screen 95.5 cm away from the field region. If the beam contains isotopes of atomic weights 39 and 41, find the separation between the points where these isotopes strike the screen. Take the mass of a potassium ion = A (1.6 × 10−27) kg, where A is the mass number.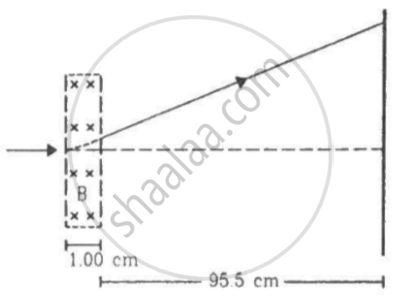
Doubly-ionised helium ions are projected with a speed of 10 km s−1 in a direction perpendicular to a uniform magnetic field of magnitude 1.0 T. Find (a) the force acting on an ion (b) the radius of the circle in which it circulates and (c) the time taken by an ion to complete the circle.
A proton is projected with a velocity of 3 × 106 m s−1 perpendicular to a uniform magnetic field of 0.6 T. Find the acceleration of the proton.
The figure shows a convex lens of focal length 12 cm lying in a uniform magnetic field Bof magnitude 1.2 T parallel to its principal axis. A particle with charge 2.0 × 10−3 C and mass 2.0 × 10−5 kg is projected perpendicular to the plane of the diagram with a speed of 4.8 m s−1. The particle moves along a circle with its centre on the principal axis at a distance of 18 cm from the lens. Show that the image of the particle moves along a circle and find the radius of that circle.

A particle with a charge of 5.0 µC and a mass of 5.0 × 10−12 kg is projected with a speed of 1.0 km s−1 in a magnetic field of magnitude 5.0 mT. The angle between the magnetic field and the velocity is sin−1 (0.90). Show that the path of the particle will be a helix. Find the diameter of the helix and its pitch.
A particle of mass m and charge q is released from the origin in a region in which the electric field and magnetic field are given by
`vecB = -B_0 vecj and vecE = E_0 vecK `
Find the speed of the particle as a function of its z-coordinate.
A long, straight wire carrying a current of 30 A is placed in an external, uniform magnetic field of 4.0 × 10−4 T parallel to the current. Find the magnitude of the resultant magnetic field at a point 2.0 cm away from the wire.
When does a moving charged particle nor experience any force while moving through a uniform magnetic field?
