Advertisements
Advertisements
Question
Two samples A and B are initially kept in the same state. Sample A is expanded through an adiabatic process and the sample B through an isothermal process. The final volumes of the samples are the same. The final pressures in A and B are pA and pBrespectively.
Options
pA > pB
pA = pB
pA < pB
The relation between pA and pB cannot be deduced.
Solution
pA < pB
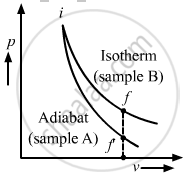
Let the initial states of samples A and B be i and the final states of samples B and A be fand f', respectively. Let the final volumes of both be Vo. As sample A is expanded through an adiabatic process, its curve in the p-V diagram is steeper than that of sampleB, which is expanded through an isothermal process. Therefore, from the p-V diagram, pA < pB.
APPEARS IN
RELATED QUESTIONS
The specific heat capacity of water is
Can we define specific heat capacity at constant temperature?
Can we define specific heat capacity for an adiabatic process?
Does a solid also have two kinds of molar heat capacities Cp and Cv? If yes, is Cp > Cv? Or is Cp − Cv = R?
Can a process on an ideal gas be both adiabatic and isothermal?
Show that the slope of the p−V diagram is greater for an adiabatic process compared to an isothermal process.
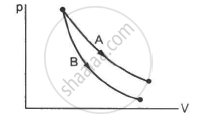
Consider the processes A and B shown in the figure. It is possible that
5 g of a gas is contained in a rigid container and is heated from 15°C to 25°C. Specific heat capacity of the gas at constant volume is 0.172 cal g−1 °C−1 and the mechanical equivalent of heat is 4.2 J cal−1. Calculate the change in the internal energy of the gas
A sample of air weighing 1.18 g occupies 1.0 × 103 cm3 when kept at 300 K and 1.0 × 105 Pa. When 2.0 cal of heat is added to it at constant volume, its temperature increases by 1°C. Calculate the amount of heat needed to increase the temperature of air by 1°C at constant pressure if the mechanical equivalent of heat is 4.2 × 107 erg cal−1. Assume that air behaves as an ideal gas.
An ideal gas expands from 100 cm3 to 200 cm3 at a constant pressure of 2.0 × 105 Pa when 50 J of heat is supplied to it. Calculate (a) the change in internal energy of the gas (b) the number of moles in the gas if the initial temperature is 300 K (c) the molar heat capacity Cp at constant pressure and (d) the molar heat capacity Cv at constant volume.
A mixture contains 1 mole of helium (Cp = 2.5 R, Cv = 1.5 R) and 1 mole of hydrogen (Cp= 3.5 R, Cv = 2.5 R). Calculate the values of Cp, Cv and γ for the mixture.
In Joly's differential steam calorimeter, 3 g of an ideal gas is contained in a rigid closed sphere at 20°C. The sphere is heated by steam at 100°C and it is found that an extra 0.095 g of steam has condensed into water as the temperature of the gas becomes constant. Calculate the specific heat capacity of the gas in J g−1 K−1. The latent heat of vaporisation of water = 540 cal g−1
Air (γ = 1.4) is pumped at 2 atm pressure in a motor tyre at 20°C. If the tyre suddenly bursts, what would be the temperature of the air coming out of the tyre? Neglect any mixing with the atmospheric air.
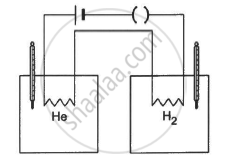
The figure shows two vessels with adiabatic walls, one containing 0.1 g of helium (γ = 1.67, M = 4 g mol−1) and the other containing some amount of hydrogen (γ = 1.4, M = 2 g mol−1). Initially, the temperatures of the two gases are equal. The gases are electrically heated for some time during which equal amounts of heat are given to the two gases. It is found that the temperatures rise through the same amount in the two vessels. Calculate the mass of hydrogen.
Molar specific heat of water is C = 74.7 J/mol K, its value in cal/g K is ______.
An engine takes in 5 moles of air at 20°C and 1 atm, and compresses it adiabatically to `1/10^"th"` of the original volume. Assuming air to be a diatomic ideal gas made up of rigid molecules, the change in its internal energy during this process comes out to be X kJ. The value of X to the nearest integer is ______.
