Advertisements
Advertisements
Question
Volume versus temperature graphs for a given mass of an ideal gas are shown in figure at two different values of constant pressure. What can be inferred about relation between P1 and P2?
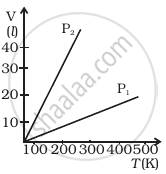
Options
P1 > P2
P1 = P2
P1 < P2
data is insufficient.
Solution
P1 > P2
Explanation:
As we know that the pressure and the quantity of gas in the system are constants. Thus, by using the ideal gas equation
PV = nRT
V ∝ T .....(When n, P and R are constants)
`V_1/T_1` = constant
Or slope of graph is constant
`V = (nRT)/P`
`(dV)/(dT) = (nR)/P`
Or `(dV)/(dT)` increases when P decreases
Thus, `(dV)/(dT) ∝ 1/P`
This shows that slope P1 is smaller than P2.
APPEARS IN
RELATED QUESTIONS
The pressure of an ideal gas is written as \[P = \frac{2E}{3V}\] . Here E refers to
0.040 g of He is kept in a closed container initially at 100.0°C. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by 12 J.
Use R = 8.3 J K-1 mol-1
Answer in brief:
A gas in a cylinder is at pressure P. If the masses of all the molecules are made one-third of their original value and their speeds are doubled, then find the resultant pressure.
Calculate the value of λmax for radiation from a body having a surface temperature of 3000 K. (b = 2.897 x 10-3 m K)
Calculate the energy radiated in one minute by a blackbody of surface area 200 cm2 at 127 °C (σ = 5.7 x 10-8 J m-2 s-1 K-4)
The average translational kinetic energy of gas molecules depends on ____________.
Average kinetic energy of H2 molecule at 300K is 'E'. At the same temperature, average kinetic energy of O2 molecule will be ______.
The molecules of a given mass of a gas have root mean square speeds of 100 ms−1 at 27°C and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and 2.0 atmospheric pressure?
23Ne decays to 23Na by negative beta emission. Mass of 23Ne is 22.994465 amu mass of 23Na is 22.989768 amu. The maximum kinetic energy of emitted electrons neglecting the kinetic energy of recoiling product nucleus is ______ MeV.
Assuming the expression for the pressure P exerted by an ideal gas, prove that the kinetic energy per unit volume of the gas is `3/2` P.
