Advertisements
Advertisements
Question
Answer in brief:
A gas in a cylinder is at pressure P. If the masses of all the molecules are made one-third of their original value and their speeds are doubled, then find the resultant pressure.
Solution
m2 = m1/3, vrms2 = 2vrms1 as the speeds of all molecules are doubled
Pressure, P = `1/3."mN"/"V"."v"^2`rms
∴ `"P"_1 = 1/3,("m"_1"N")/"V"."v"_"rms 1"^2` and
∴ `"P"_2 = 1/3,("m"_2"N")/"V"."v"_"rms 2"^2`
∴ `"P"_2/"P"_1 = ("m"_2/"m"_1)(("v"_"rms2"^2)/("v"_"rms 1"^2))`
`=("m"_2/"m"_1)(("v"_"rms 2")/("v"_"rms 1"))^2`
`= (("m"_1//3)/"m"_1)(2)^2 = 4/3`
∴ `"P"_2 = 4/3"P"_1 = 4/3"P"`
This is the resultant pressure.
APPEARS IN
RELATED QUESTIONS
Can we define the temperature of (a) vacuum, (b) a single molecule?
Which of the following quantities is the same for all ideal gases at the same temperature?
(a) The kinetic energy of 1 mole
(b) The kinetic energy of 1 g
(c) The number of molecules in 1 mole
(d) The number of molecules in 1 g
0.040 g of He is kept in a closed container initially at 100.0°C. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by 12 J.
Use R = 8.3 J K-1 mol-1
An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
Figure shows a cylindrical tube of cross-sectional area A fitted with two frictionless pistons. The pistons are connected to each other by a metallic wire. Initially, the temperature of the gas is T0 and its pressure is p0 which equals the atmospheric pressure. (a) What is the tension in the wire? (b) What will be the tension if the temperature is increased to 2T0 ?

The weather report reads, "Temperature 20°C : Relative humidity 100%". What is the dew point?
The temperature and the dew point in an open room are 20°C and 10°C. If the room temperature drops to 15°C, what will be the new dew point?
If a = 0.72 and r = 0.24, then the value of tr is ______.
At what temperature will oxygen molecules have same rms speed as helium molecules at S.T.P.? (Molecular masses of oxygen and helium are 32 and 4 respectively).
If the density of oxygen is 1.44 kg/m3 at a pressure of 105 N/m2, find the root mean square velocity of oxygen molecules.
Calculate the ratio of the mean square speeds of molecules of a gas at 30 K and 120 K.
Energy is emitted from a hole in an electric furnace at the rate of 20 W when the temperature of the furnace is 727°C. What is the area of the hole? (Take Stefan’s constant σ to be 5.7 × 10-8 Js-1 m-2K-4.)
Earth’s mean temperature can be assumed to be 280 K. How will the curve of blackbody radiation look like for this temperature? Find out λmax. In which part of the electromagnetic spectrum, does this value lie? (Take Wien's constant b = 2.897 × 10−3 m K)
Calculate the energy radiated in one minute by a blackbody of surface area 200 cm2 at 127 °C (σ = 5.7 x 10-8 J m-2 s-1 K-4)
If the density of nitrogen is 1.25 kg/m3 at a pressure of 105 Pa, find the root mean square velocity of nitrogen molecules.
A metal cube of length 4 cm radiates heat at the rate of 10 J/s. Find its emissive power at a given temperature.
What is the microscopic origin of temperature?
When photons of energy hv fall on a metal plate of work function 'W0', photoelectrons of maximum kinetic energy 'K' are ejected. If the frequency of the radiation is doubled, the maximum kinetic energy of the ejected photoelectrons will be ______.
The average K.E. of hydrogen molecules at 27° C is E. The average K.E. at 627° C is ____________.
The average translational kinetic energy of a molecule in a gas becomes equal to 0.49 eV at a temperature about (Boltzmann constant = 1.38 x 10-23 JK-1) ____________.
Assuming the expression for the pressure exerted by the gas on the wall of the container, it can be shown that pressure is ______.
A molecule consists of two atoms each of mass 'm' and separated by a distance 'd'. At room temperature the average rotational kinetic energy is 'E', then its angular frequency is ______.
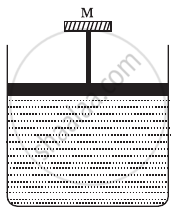
A cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (Figure). If the temperature is increased ______.
The molecules of a given mass of a gas have root mean square speeds of 100 ms−1 at 27°C and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and 2.0 atmospheric pressure?
A proton, a deuteron and an α-particle with same kinetic energy enter into a uniform magnetic field at right angle to magnetic field. The ratio of the radii of their respective circular paths is ______.
For a particle moving in vertical circle, the total energy at different positions along the path ______.
Assuming the expression for the pressure P exerted by an ideal gas, prove that the kinetic energy per unit volume of the gas is `3/2` P.
