Advertisements
Advertisements
Question
At what temperature will oxygen molecules have same rms speed as helium molecules at S.T.P.? (Molecular masses of oxygen and helium are 32 and 4 respectively).
Solution
Given: Standard Temperature Pressure (S.T.P) i.e. T2 = 273 K, M01 (oxygen) = 32 × 10-3 kg/mol, M02 (helium) = 4 × 10-3 kg/mol,
`"v"_"rms" = sqrt("3RT"/"M"_0)`
The rms speed of oxygen molecules, `"v"_1 = sqrt("3RT"_1/"M"_01)` and that of helium molecules,
`"v"_2 = sqrt("3RT"_2/"M"_02)`
when v1 = v2 ,
`sqrt("3RT"_1/"M"_01) = sqrt("3RT"_2/"M"_02)`
`∴ "T"_1/"M"_01 = "T"_2/"M"_02`
∴ Temperature, T1 = `"M"_01/"M"_02. "T"_2`
`= ((32 xx 10^-3)(273))/(4 xx 10^-3)`
= 2184 K
APPEARS IN
RELATED QUESTIONS
Do you expect the gas in a cooking gas cylinder to obey the ideal gas equation?
If the molecules were not allowed to collide among themselves, would you expect more evaporation or less evaporation?
The mean square speed of the molecules of a gas at absolute temperature T is proportional to
The average translational kinetic energy of air molecules is 0.040 eV (1 eV = 1.6 × 10−19J). Calculate the temperature of the air. Boltzmann constant k = 1.38 × 10−23 J K−1.
0.040 g of He is kept in a closed container initially at 100.0°C. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by 12 J.
Use R = 8.3 J K-1 mol-1
An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
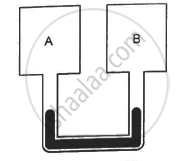
Figure shows two rigid vessels A and B, each of volume 200 cm3, containing an ideal gas (Cv = 12.5 J K−1 mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K. (a) Find the number of moles of the gas in each vessel. (b) 5.0 J of heat is supplied to the gas in vessel A and 10 J to the gas in vessel B. Assuming there's no appreciable transfer of heat from A to B, calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant, R = 8.3 J K−1 mol−1.
A glass contains some water at room temperature 20°C. Refrigerated water is added to it slowly. when the temperature of the glass reaches 10°C, small droplets condense on the outer surface. Calculate the relative humidity in the room. The boiling point of water at a pressure of 17.5 mm of mercury is 20°C and at 8.9 mm of mercury it is 10°C.
Answer in brief:
A gas in a cylinder is at pressure P. If the masses of all the molecules are made one-third of their original value and their speeds are doubled, then find the resultant pressure.
When a gas is heated, its temperature increases. Explain this phenomenon on the basis of the kinetic theory of gases.
Two vessels A and B are filled with the same gas where the volume, temperature, and pressure in vessel A is twice the volume, temperature, and pressure in vessel B. Calculate the ratio of the number of molecules of the gas in vessel A to that in vessel B.
Earth’s mean temperature can be assumed to be 280 K. How will the curve of blackbody radiation look like for this temperature? Find out λmax. In which part of the electromagnetic spectrum, does this value lie? (Take Wien's constant b = 2.897 × 10−3 m K)
Calculate the value of λmax for radiation from a body having a surface temperature of 3000 K. (b = 2.897 x 10-3 m K)
Compare the rate of radiation of metal bodies at 727 °C and 227 °C.
The average K.E. of hydrogen molecules at 27° C is E. The average K.E. at 627° C is ____________.
A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity `omega`. Its kinetic energy is ______.
Average kinetic energy of H2 molecule at 300K is 'E'. At the same temperature, average kinetic energy of O2 molecule will be ______.
The average translational kinetic energy of a molecule in a gas is 'E1'. The kinetic energy of the electron (e) accelerated from rest through p.d. 'V' volt is 'E2'. The temperature at which E1 = E2 is possible, is ______.
An inflated rubber balloon contains one mole of an ideal gas, has a pressure p, volume V and temperature T. If the temperature rises to 1.1 T, and the volume is increased to 1.05 V, the final pressure will be ______.
The molecules of a given mass of a gas have root mean square speeds of 100 ms−1 at 27°C and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and 2.0 atmospheric pressure?
Two molecules of a gas have speeds of 9 × 10 6 ms−1 and 1 × 106 ms−1, respectively. What is the root mean square speed of these molecules?
A gas mixture consists of molecules of types A, B and C with masses mA > mB > mC. Rank the three types of molecules in decreasing order of rms speeds.
23Ne decays to 23Na by negative beta emission. Mass of 23Ne is 22.994465 amu mass of 23Na is 22.989768 amu. The maximum kinetic energy of emitted electrons neglecting the kinetic energy of recoiling product nucleus is ______ MeV.
The Q-value of a nuclear reaction and kinetic energy of the projectile particle, KP are related as ______.
For a particle moving in vertical circle, the total energy at different positions along the path ______.
According to the kinetic theory of gases, at a given temperature, molecules of all gases have the same ______.
If a = 0. 72 and t = 0.04, then the value of r is ______.
2000 calories of radiant heat is incident on a body. If the body absorbs 550 calories of heat, find the coefficient of emmission of the body.
