Advertisements
Advertisements
Question
Figure shows two rigid vessels A and B, each of volume 200 cm3, containing an ideal gas (Cv = 12.5 J K−1 mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K. (a) Find the number of moles of the gas in each vessel. (b) 5.0 J of heat is supplied to the gas in vessel A and 10 J to the gas in vessel B. Assuming there's no appreciable transfer of heat from A to B, calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant, R = 8.3 J K−1 mol−1.
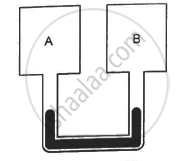
Solution
Given:
Volume of gas in each vessel, V = 200 cm3
Specific heat at constant volume of the gas, Cv = 12.5 J/mol-K
Initial temperature of the gas, T = 300 K
Initial pressure of the gas, P = 75 cm of Hg
(a) Using the ideal gas equation, number of moles of gases in each vessel,
75 cm of Hg = 99991.5 N/m2
`"n" = ("P""V")/("R""T")`
`= (99991.5 xx 200 xx 10^-6)/(8.3 xx 300)`
= 8031.4 xx 10-6
=0.008
(b) Heat is supplied to the gas, but dV is zero as the container has rigid walls.
So, dW = P Δ V = 0
From first law of thermodynamics,
dQ = dU
⇒ 5 = nCvdT
⇒ 5 = 0.008 × 12.5 × dT
⇒ dT = 50 for A
`"P"/"T" = "P"_"A"/"T"_"A" ` because volume is kept constant.
Q = nCvdT
`"T" = "Q"/("n""C"_"v")`
`75/300 =( "P"_"A" xx 0.008 xx 12.5)/5`
`"P"_"A" = (75 xx 5)/(300 xx 0.008 xx 12.5)`
= 12.5 cm of Hg
Again ,` "P"/"T" = "P"_"B"/"T"_"B" [ For container B]`
`75/300 =( "P"_"B" xx 0.008 xx 12.5 )/10`
PB = 25 cm of Hg
The distance moved by the mercury,
PB − PA = 25 − 12.5 = 12.5 cm
APPEARS IN
RELATED QUESTIONS
When we place a gas cylinder on a van and the van moves, does the kinetic energy of the molecules increase? Does the temperature increase?
The process on an ideal gas, shown in figure, is
A gas cylinder has walls that can bear a maximum pressure of 1.0 × 106 Pa. It contains a gas at 8.0 × 105 Pa and 300 K. The cylinder is steadily heated. Neglecting any change in the volume, calculate the temperature at which the cylinder will break.
The mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.
Use R = 8.314 JK-1 mol-1
During an experiment, an ideal gas is found to obey an additional law pV2 = constant. The gas is initially at a temperature T and volume V. Find the temperature when it expands to a volume 2V.
Use R = 8.3 J K-1 mol-1
Figure shows two vessels A and B with rigid walls containing ideal gases. The pressure, temperature and the volume are pA, TA, V in the vessel A and pB, TB, V in the vessel B. The vessels are now connected through a small tube. Show that the pressure p and the temperature T satisfy `Ρ/T = 1/2 ({P_A}/{T_A}+{P_B}/{T_B))` when equilibrium is achieved.

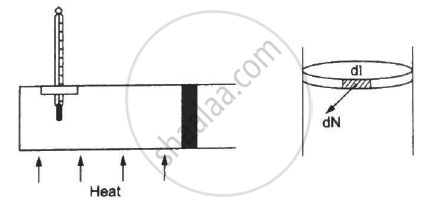
Figure shows a cylindrical tube of radius 5 cm and length 20 cm. It is closed by a tight-fitting cork. The friction coefficient between the cork and the tube is 0.20. The tube contains an ideal gas at a pressure of 1 atm and a temperature of 300 K. The tube is slowly heated and it is found that the cork pops out when the temperature reaches 600 K. Let dN denote the magnitude of the normal contact force exerted by a small length dlof the cork along the periphery (see the figure). Assuming that the temperature of the gas is uniform at any instant, calculate `(dN)/(dt)`.
If a = 0.72 and r = 0.24, then the value of tr is ______.
Answer in brief:
Show that rms velocity of an oxygen molecule is `sqrt2` times that of a sulfur dioxide molecule at S.T.P.
At what temperature will oxygen molecules have same rms speed as helium molecules at S.T.P.? (Molecular masses of oxygen and helium are 32 and 4 respectively).
Earth’s mean temperature can be assumed to be 280 K. How will the curve of blackbody radiation look like for this temperature? Find out λmax. In which part of the electromagnetic spectrum, does this value lie? (Take Wien's constant b = 2.897 × 10−3 m K)
Calculate the energy radiated in one minute by a blackbody of surface area 200 cm2 at 127 °C (σ = 5.7 x 10-8 J m-2 s-1 K-4)
On what, the values of absorption coefficient, reflection coefficient, and transmission coefficient depend, in addition to the material of the object on which the radiation is an incident?
Above what temperature, all bodies radiate electromagnetic radiation?
Explain in detail the kinetic interpretation of temperature.
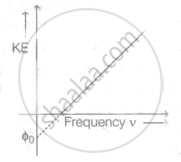
The graph of kinetic energy against the frequency v of incident light is as shown in the figure. The slope of the graph and intercept on X-axis respectively are ______.
A cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (Figure). If the temperature is increased ______.
An inflated rubber balloon contains one mole of an ideal gas, has a pressure p, volume V and temperature T. If the temperature rises to 1.1 T, and the volume is increased to 1.05 V, the final pressure will be ______.
The molecules of a given mass of a gas have root mean square speeds of 100 ms−1 at 27°C and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and 2.0 atmospheric pressure?
The Q-value of a nuclear reaction and kinetic energy of the projectile particle, KP are related as ______.
