Advertisements
Advertisements
Question
Explain in detail the kinetic interpretation of temperature.
Solution
To understand the microscopic origin of temperature in the same way, from pressure exerted by a gas,
P = `1/3 "N"/"V""m"bar("v"^2)`
PV = `1/3"Nm"bar("v"^2)` ............(1)
Comparing the equation (1) with the ideal gas equation PV = NkT,
NkT = `1/3"Nm"bar("v"^2)`
kT = `1/3"m"bar("v"^2)` .........(2)
Multiply the above equation by `3/2` on both sides,
`3/2"kT" = 1/2"m"bar("v"^2)` ...........(3)
R.H.S. of the equation (3) is called average kinetic energy of a single molecule `(bar"KE")`.
The average kinetic energy per molecule
`bar"KE"` = ∈ = `3/2"kT"` ...........(4)
Equation (3) implies that the temperature, of a gas, is a measure of the average translational kinetic energy per molecule of the gas.
Equation (4) is a very important result of the kinetic theory of gas. We can infer the following from this equation.
(i) The average kinetic energy of the molecule is directly proportional to the absolute temperature of the gas. Equation (3) gives the connection between the macroscopic world (temperature) to the microscopic world (motion of molecules).
(ii) The average kinetic energy of each molecule depends only on the temperature of the gas hot on the mass of the molecule. In other words, if the temperature of an ideal gas is measured using the thermometer, the average kinetic energy of each molecule can be calculated without seeing the molecule through the naked eye.
By multiplying the total number of gas molecules with the average kinetic energy of each molecule, the internal energy of the gas is obtained.
Internal energy of ideal gas U = `"N"(1/2"m"bar("v"^2))"`
By using equation (3), U = `3/2"NkT"` ..........(5)
Here, we understand that the internal energy of an ideal gas depends only on absolute temperature and is independent of pressure and volume.
APPEARS IN
RELATED QUESTIONS
Do you expect the gas in a cooking gas cylinder to obey the ideal gas equation?
0.040 g of He is kept in a closed container initially at 100.0°C. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by 12 J.
Use R = 8.3 J K-1 mol-1
Figure shows a cylindrical tube of cross-sectional area A fitted with two frictionless pistons. The pistons are connected to each other by a metallic wire. Initially, the temperature of the gas is T0 and its pressure is p0 which equals the atmospheric pressure. (a) What is the tension in the wire? (b) What will be the tension if the temperature is increased to 2T0 ?

An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg in figure. The vessel itself is kept in a big chamber containing air at atmospheric pressure 100 kPa. The length of the gas column is 20 cm. If the chamber is now completely evacuated by an exhaust pump, what will be the length of the gas column? Assume the temperature to remain constant throughout the process.
The weather report reads, "Temperature 20°C : Relative humidity 100%". What is the dew point?
Earth’s mean temperature can be assumed to be 280 K. How will the curve of blackbody radiation look like for this temperature? Find out λmax. In which part of the electromagnetic spectrum, does this value lie? (Take Wien's constant b = 2.897 × 10−3 m K)
An ideal gas in a container of volume 500 cc is at a pressure of 2 × 105 N/m2. The average kinetic energy of each molecule is 6 × 10−21 J. The number of gas molecules in the container is ______.
A cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (Figure). If the temperature is increased ______.
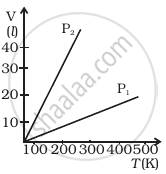
Volume versus temperature graphs for a given mass of an ideal gas are shown in figure at two different values of constant pressure. What can be inferred about relation between P1 and P2?
If a = 0. 72 and t = 0.04, then the value of r is ______.
