Advertisements
Advertisements
Questions
Derive an expression for the pressure exerted by a gas on the basis of the kinetic theory of gases.
On the basis of the kinetic theory of gases obtain an expression for pressure exerted by gas molecules enclosed in a container on its walls.
Solution 1
Expression for pressure exerted by a gas:
Consider a monoatomic gas of N molecules each having a mass m inside a cubical container of side l.
The molecules of the gas are in random motion. They collide with each other and also with the walls of the container. As the collisions are elastic in nature, there is no loss of energy, but a change in momentum occurs.

Container of gas molecules

Collision of a molecule with the wall
The molecules of the gas exert pressure on the walls of the container due to the collision on it. During each collision, the molecules impart certain momentum to the wall. Due to the transfer of momentum, the walls experience a continuous force. The force experienced per unit area of the walls of the container determines the pressure exerted by the gas. It is essential to determine the total momentum transferred by the molecules in a short interval of time.
A molecule of mass m moving with a velocity `vec"v"` having components (vx, vy, vz) hits the right side wall. Since we have assumed that the collision is elastic, the particle rebounds with the same speed and its x-component are reversed. This is shown in the figure. The components of velocity of the molecule after the collision are (- vx, vy, vz).
The x-component of momentum of the molecule before collision = mvx
The x-component of momentum of the molecule after collision = – mvx
The change in momentum of the molecule in x-direction = Final momentum – initial momentum
= – mvx – mvx
= – 2mvx
According to the law of conservation of linear momentum, the change in momentum of the wall = 2mvx
The number of molecules hitting the right side wall in a small interval of time At.
The molecules within the distance of vx∆t from the right side wall and moving towards the right will hit the wall in the time interval ∆t. The number of molecules that will hit the right side wall in a time interval At is equal to the product of volume (Avx∆t) and number density of the molecules (n). Here A is an area of the wall and n is the number of molecules per unit volume `"N"/"V"`.
We have assumed that the number density is the same throughout the cube.

Number of molecules hitting the wall
Not all the n molecules will move to the right, therefore on average only half of the n molecules move to the right and the other half moves towards the left side.
The number of molecules that hit the right side wall in a time interval ∆t
= `"n"/2"` Avx∆t ..............(1)
In the same interval of time At, the total momentum transferred by the molecules
∆P = `"n"/2"Av"_"x"Δ"t" xx 2"mv"_"x" = "Av"_"x"^2"mn"Δ"t"` .......(2)
From Newton’s second law, the change in momentum in a small interval of time gives rise to force.
The force exerted by the molecules on the wall (in magnitude)
F = `(Δ"P")/(Δ"t") = "nmAv"_"x"^2` ...........(3)
Pressure, P = force divided by the area of the wall
P = `"F"/"A" = "nmv"_"x"^2` ..................(4)
Since all the molecules are moving completely in a random manner, they do not have the same speed. So we can replace the term `"v"_"x"^2` with the average `bar("v"_"x"^2)` in equation (4).
P = `"nm"bar("v"_"x"^2)` ........(5)
Since the gas is assumed to move in a random direction, it has no preferred direction of motion (the effect of gravity on the molecules is neglected). It implies that the molecule has the same average speed in all three directions. So, `bar("v"_"x"^2) = bar("v"_"y"^2) = bar("v"_"z"^2)`. The mean square speed is written as
`bar("v"^2) = bar("v"_"x"^2) + bar("v"_"y"^2) + bar("v"_"z"^2) = 3bar("v"_"x"^2)`
`bar("v"_"x"^2) = 1/3 bar("v"^2)`
Using this in equation (5), we get
P = `1/3"nm"bar("v"^2)` or P = `1/3 "N"/"V" "m"bar("v"^2)` ...........(6)
as `["n" = "N"/"V"]`
Solution 2
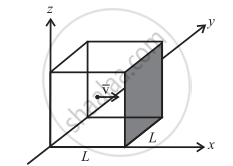
Let there be n moles of an ideal gas enclosed in a cubical box of volume V = L3 and constant temperature T.
The molecule is moving with the velocity V and collides with the shaded wall of the cube. The wall is Parallel to the yz plane. The change in momentum of the X-component is
ΔPx = final momentum - initial momentum
= (-mvx) - (mvx)
= -2 mvx
The momentum transferred to the wall is +2mvx in magnitude. The rebounded molecule then goes to the opposite wall and collides with it.
As L is the length of the cubical box, the time for the molecule to travel back and forth to the shaded wall is
`(Delta "t" = (2"L")/"V"_x)`.
The average force exerted on the shaded wall by molecule 1 is given as:
Average force = Average rate of change of momentum
`= (2"mv"_(x1))/(Delta"L"//"V"_(x1)) = "mv"_(x1)^2/"L"`
The total average force on the wall from all molecules is
`= "m"/"L" ("v"_(x1)^2 + "v"_(x2)^2 + "v"_(x3)^3 + ...)`
∴ The average pressure
P = `"Average force"/"Area of the shaded wall"`
`= ("m"("v"_(x1)^2 + "v"_(x2)^2 + "v"_(x3)^3 + ...))/"LL"^2`
P = `"m"/"L"^3 ("V"_(x1)^2 + "V"_(x2)^2 + "V"_(x3)^2 + ...)`
The average of the square of x component of the velocities is given by:
`overline("V"_x^2) = ("V"_(x1)^2 + "V"_(x2)^2 + "V"_(x3)^2 + ... + "V"_("N")^2)/"N"`
∴ P = `("mN" overline("v"_x^(2)))/"V"` ...(L3 = V)
Now `overline("V"^2) = overline("V"_x^2) + overline("V"_"y"^2) + overline("V"_"z"^2)`
By symmetry,
`overline("V"_x^2) = overline("V"_y^2) = overline("V"_z^2) = 1/3 overline("V"^2)`
Since the molecule has no preferred direction to move.
∴ Average Pressure
P = `1/3 "N"/"V" "m"overline("v"^2)`
P = `1/3 rho overline("V"^2)`
This is the required expression of pressure exerted by a gas.
RELATED QUESTIONS
Find the kinetic energy of 3 litre of gas at S.T.P given standard pressure is 1.013 × 105 N/m2.
Determine the pressure of nitrogen at 0°C if the density of nitrogen at N.T.P. is 1.25 kg/m3 and R.M.S. speed of the molecules at N.T.P. is 489 m/s.
A sample of an ideal gas is at equilibrium. Which of the following quantity is zero?
Two identically sized rooms A and B are connected by an open door. If the room A is air-conditioned such that its temperature is 4°C lesser than room B, which room has more air in it?
If the internal energy of an ideal gas U and volume V are doubled then the pressure ____________.
The ratio γ = `"C"_"p"/"C"_"v"` for a gas mixture consisting of 8 g of helium and 16 g of oxygen is ____________.
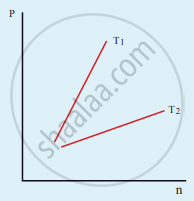
The following graph represents the pressure versus number density for an ideal gas at two different temperatures T1 and T2. The graph implies
What is the microscopic origin of pressure?
A gas is at temperature 80°C and pressure 5 × 10−10 Nm−2. What is the number of molecules per m3 if Boltzmann’s constant is 1.38 × 10−23 J K−1
If 1020 oxygen molecules per second strike 4 cm2 of wall at an angle of 30° with the normal when moving at a speed of 2 × 103 ms−1, find the pressure exerted on the wall. (mass of one oxygen atom = 2.67 × 10−26 kg)
Estimate the total number of air molecules in a room of a capacity of 25 m3 at a temperature of 27°C.
According to the assumptions made in the kinetic theory of gases, when two molecules of a gas collide with each other, then ______.
The average force applied on the walls of a closed container depends as 'Tx', where 'T' is the temperature of an ideal gas. The value of 'x' is ______.
What is an ideal gas?
Does an ideal gas exist in practice?
The kinetic energy per molecule of a gas at temperature T is ______.
Temperature remaining constant, if you double the number of molecules in a box, the pressure will ______.
The velocities of five molecules are 2 m/s, 3 m/s, 4 m/s, 5 m/s and 6 m/s. Find the root mean square velocity of molecules.
