Advertisements
Advertisements
प्रश्न
Explain in detail the kinetic interpretation of temperature.
उत्तर
To understand the microscopic origin of temperature in the same way, from pressure exerted by a gas,
P = `1/3 "N"/"V""m"bar("v"^2)`
PV = `1/3"Nm"bar("v"^2)` ............(1)
Comparing the equation (1) with the ideal gas equation PV = NkT,
NkT = `1/3"Nm"bar("v"^2)`
kT = `1/3"m"bar("v"^2)` .........(2)
Multiply the above equation by `3/2` on both sides,
`3/2"kT" = 1/2"m"bar("v"^2)` ...........(3)
R.H.S. of the equation (3) is called average kinetic energy of a single molecule `(bar"KE")`.
The average kinetic energy per molecule
`bar"KE"` = ∈ = `3/2"kT"` ...........(4)
Equation (3) implies that the temperature, of a gas, is a measure of the average translational kinetic energy per molecule of the gas.
Equation (4) is a very important result of the kinetic theory of gas. We can infer the following from this equation.
(i) The average kinetic energy of the molecule is directly proportional to the absolute temperature of the gas. Equation (3) gives the connection between the macroscopic world (temperature) to the microscopic world (motion of molecules).
(ii) The average kinetic energy of each molecule depends only on the temperature of the gas hot on the mass of the molecule. In other words, if the temperature of an ideal gas is measured using the thermometer, the average kinetic energy of each molecule can be calculated without seeing the molecule through the naked eye.
By multiplying the total number of gas molecules with the average kinetic energy of each molecule, the internal energy of the gas is obtained.
Internal energy of ideal gas U = `"N"(1/2"m"bar("v"^2))"`
By using equation (3), U = `3/2"NkT"` ..........(5)
Here, we understand that the internal energy of an ideal gas depends only on absolute temperature and is independent of pressure and volume.
APPEARS IN
संबंधित प्रश्न
It is said that the assumptions of kinetic theory are good for gases having low densities. Suppose a container is so evacuated that only one molecule is left in it. Which of the assumptions of kinetic theory will not be valid for such a situation? Can we assign a temperature to this gas?
The average translational kinetic energy of air molecules is 0.040 eV (1 eV = 1.6 × 10−19J). Calculate the temperature of the air. Boltzmann constant k = 1.38 × 10−23 J K−1.
One mole of an ideal gas undergoes a process `P = (P_0)/(1+(V/V_0)^2` where `p_0` and `V_0` are constants . Find the temperature of the gas when `V=V_0` .
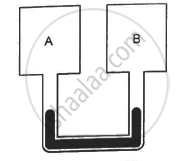
Figure shows two rigid vessels A and B, each of volume 200 cm3, containing an ideal gas (Cv = 12.5 J K−1 mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K. (a) Find the number of moles of the gas in each vessel. (b) 5.0 J of heat is supplied to the gas in vessel A and 10 J to the gas in vessel B. Assuming there's no appreciable transfer of heat from A to B, calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant, R = 8.3 J K−1 mol−1.
Answer in brief:
A gas in a cylinder is at pressure P. If the masses of all the molecules are made one-third of their original value and their speeds are doubled, then find the resultant pressure.
Compare the rates of emission of heat by a blackbody maintained at 727°C and at 227°C, if the black bodies are surrounded by an enclosure (black) at 27°C. What would be the ratio of their rates of loss of heat?
The number of degrees of freedom, for the vibrational motion of a polyatomic molecule, depends on the ______
An ideal gas in a container of volume 500 cc is at a pressure of 2 × 105 N/m2. The average kinetic energy of each molecule is 6 × 10−21 J. The number of gas molecules in the container is ______.
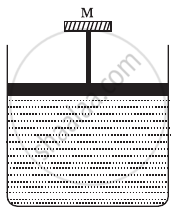
A cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (Figure). If the temperature is increased ______.
Show that the average energy per molecule is proportional to the absolute temperature T of the gas.
