Advertisements
Advertisements
Question
Answer in brief:
Show that rms velocity of an oxygen molecule is `sqrt2` times that of a sulfur dioxide molecule at S.T.P.
Solution
`("M"_0 ("SO"_2))/("M"_0 ("O"_2)) = (64 "kg/mol")/(32 "kg/mol") = 2`
The rms speed, `"v"_"rms" = sqrt("3RT"/"M"_0)`
∴ `"v"_"rms" ∝ 1/sqrt"M"_0` at constant T
∴ `("v"_"rms"("O"_2))/("v"_"rms"("SO"_2)) = sqrt(("M"_0 ("SO"_2))/("M"_0 ("O"_2))) = sqrt2`
Thus, `"v"_"rms"("O"_2) = sqrt2 "v"_"rms"("SO"_2)`
APPEARS IN
RELATED QUESTIONS
A gas is kept in an enclosure. The pressure of the gas is reduced by pumping out some gas. Will the temperature of the gas decrease by Charles's low?
If the molecules were not allowed to collide among themselves, would you expect more evaporation or less evaporation?
Is it possible to boil water at room temperature, say 30°C? If we touch a flask containing water boiling at this temperature, will it be hot?
The mean square speed of the molecules of a gas at absolute temperature T is proportional to
A gas cylinder has walls that can bear a maximum pressure of 1.0 × 106 Pa. It contains a gas at 8.0 × 105 Pa and 300 K. The cylinder is steadily heated. Neglecting any change in the volume, calculate the temperature at which the cylinder will break.
At what temperature the mean speed of the molecules of hydrogen gas equals the escape speed from the earth?
Use R = 8.314 JK-1 mol-1
Figure shows two vessels A and B with rigid walls containing ideal gases. The pressure, temperature and the volume are pA, TA, V in the vessel A and pB, TB, V in the vessel B. The vessels are now connected through a small tube. Show that the pressure p and the temperature T satisfy `Ρ/T = 1/2 ({P_A}/{T_A}+{P_B}/{T_B))` when equilibrium is achieved.

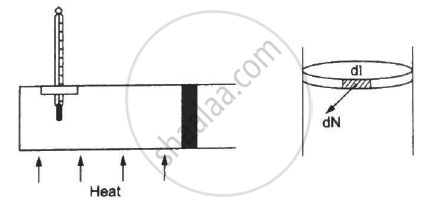
Figure shows a cylindrical tube of radius 5 cm and length 20 cm. It is closed by a tight-fitting cork. The friction coefficient between the cork and the tube is 0.20. The tube contains an ideal gas at a pressure of 1 atm and a temperature of 300 K. The tube is slowly heated and it is found that the cork pops out when the temperature reaches 600 K. Let dN denote the magnitude of the normal contact force exerted by a small length dlof the cork along the periphery (see the figure). Assuming that the temperature of the gas is uniform at any instant, calculate `(dN)/(dt)`.
The weather report reads, "Temperature 20°C : Relative humidity 100%". What is the dew point?
A glass contains some water at room temperature 20°C. Refrigerated water is added to it slowly. when the temperature of the glass reaches 10°C, small droplets condense on the outer surface. Calculate the relative humidity in the room. The boiling point of water at a pressure of 17.5 mm of mercury is 20°C and at 8.9 mm of mercury it is 10°C.
An adiabatic cylindrical tube of cross-sectional area 1 cm2 is closed at one end and fitted with a piston at the other end. The tube contains 0.03 g of an ideal gas. At 1 atm pressure and at the temperature of the surrounding, the length of the gas column is 40 cm. The piston is suddenly pulled out to double the length of the column. The pressure of the gas falls to 0.355 atm. Find the speed of sound in the gas at atmospheric temperature.
At what temperature will oxygen molecules have same rms speed as helium molecules at S.T.P.? (Molecular masses of oxygen and helium are 32 and 4 respectively).
Answer in brief:
Compare the rms speed of hydrogen molecules at 127ºC with rms speed of oxygen molecules at 27ºC given that molecular masses of hydrogen and oxygen are 2 and 32 respectively.
Calculate the ratio of the mean square speeds of molecules of a gas at 30 K and 120 K.
Calculate the average molecular kinetic energy
- per kmol
- per kg
- per molecule
of oxygen at 127°C, given that the molecular weight of oxygen is 32, R is 8.31 J mol−1K−1 and Avogadro’s number NA is 6.02 × 1023 molecules mol−1.
Energy is emitted from a hole in an electric furnace at the rate of 20 W when the temperature of the furnace is 727°C. What is the area of the hole? (Take Stefan’s constant σ to be 5.7 × 10-8 Js-1 m-2K-4.)
Compare the rates of emission of heat by a blackbody maintained at 727°C and at 227°C, if the black bodies are surrounded by an enclosure (black) at 27°C. What would be the ratio of their rates of loss of heat?
Calculate the energy radiated in one minute by a blackbody of surface area 200 cm2 at 127 °C (σ = 5.7 x 10-8 J m-2 s-1 K-4)
Explain in detail the kinetic interpretation of temperature.
A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity `omega`. Its kinetic energy is ______.
Average kinetic energy of H2 molecule at 300K is 'E'. At the same temperature, average kinetic energy of O2 molecule will be ______.
The average translational kinetic energy of a molecule in a gas is 'E1'. The kinetic energy of the electron (e) accelerated from rest through p.d. 'V' volt is 'E2'. The temperature at which E1 = E2 is possible, is ______.
Two molecules of a gas have speeds of 9 × 10 6 ms−1 and 1 × 106 ms−1, respectively. What is the root mean square speed of these molecules?
An insulated container containing monoatomic gas of molar mass m is moving with a velocity vo. If the container is suddenly stopped, find the change in temperature.
Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. Assume the velocity is along x-axis and the area of cross-section of the block perpendicular to v0 is A. Show that the drag force on the block is `4ρAv_0 sqrt((KT)/m)`, where m is the mass of the gas molecule.
The Q-value of a nuclear reaction and kinetic energy of the projectile particle, KP are related as ______.
When a particle oscillates simple harmonically, its kinetic energy varies periodically. If frequency of the particle is n, then the frequency of the kinetic energy is ______.
Assuming the expression for the pressure P exerted by an ideal gas, prove that the kinetic energy per unit volume of the gas is `3/2` P.
