Advertisements
Advertisements
Question
Calculate the average molecular kinetic energy
- per kmol
- per kg
- per molecule
of oxygen at 127°C, given that the molecular weight of oxygen is 32, R is 8.31 J mol−1K−1 and Avogadro’s number NA is 6.02 × 1023 molecules mol−1.
Solution
Data: T = 273 + 127 = 400 K,
molecular weight = 32
∴ molar mass = 32 kg/kmol,
R = 8.31 Jmol-1K-1,
NA = 6.02 × 1023 molecules mol-1
(i) The average molecular kinetic energy per kmol of oxygen = the average kinetic energy per mol of oxygen × 1000
`= 3/2 "RT" xx 1000`
= `3/2(8.31)(400)(10^3)"J"/"kmol"`
= (600)(8.31)(103)
= 4.986 × 106 J/kmol
(ii) The average molecular kinetic energy per kg of oxygen
= `3/2 "RT"/"M"_0`
= `(4.986xx10^6 "J"//"mol")/(32 "kg"//"kmol")`
= 1.558 × 105 J/kg.
(iii) The average molecular kinetic energy per molecule of oxygen
= `3/2 "RT"/"N"_"A"`
= `(4.986 xx 10^6 "J"//"mol")/(6.02 xx 10^23 "molecule"//"mol")`
= 8.282 × 10-21 J/molecule
APPEARS IN
RELATED QUESTIONS
When we place a gas cylinder on a van and the van moves, does the kinetic energy of the molecules increase? Does the temperature increase?
Do you expect the gas in a cooking gas cylinder to obey the ideal gas equation?
Consider a gas of neutrons. Do you expect it to behave much better as an ideal gas as compared to hydrogen gas at the same pressure and temperature?
If the molecules were not allowed to collide among themselves, would you expect more evaporation or less evaporation?
Is it possible to boil water at room temperature, say 30°C? If we touch a flask containing water boiling at this temperature, will it be hot?
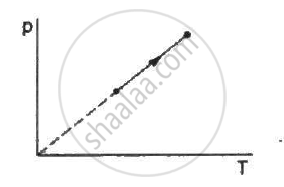
The process on an ideal gas, shown in figure, is
Which of the following quantities is the same for all ideal gases at the same temperature?
(a) The kinetic energy of 1 mole
(b) The kinetic energy of 1 g
(c) The number of molecules in 1 mole
(d) The number of molecules in 1 g
A gas cylinder has walls that can bear a maximum pressure of 1.0 × 106 Pa. It contains a gas at 8.0 × 105 Pa and 300 K. The cylinder is steadily heated. Neglecting any change in the volume, calculate the temperature at which the cylinder will break.
0.040 g of He is kept in a closed container initially at 100.0°C. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by 12 J.
Use R = 8.3 J K-1 mol-1
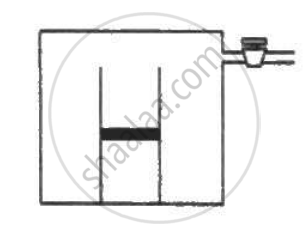
An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg in figure. The vessel itself is kept in a big chamber containing air at atmospheric pressure 100 kPa. The length of the gas column is 20 cm. If the chamber is now completely evacuated by an exhaust pump, what will be the length of the gas column? Assume the temperature to remain constant throughout the process.
The weather report reads, "Temperature 20°C : Relative humidity 100%". What is the dew point?
Using figure, find the boiling point of methyl alcohol at 1 atm (760 mm of mercury) and at 0.5 atm.

A glass contains some water at room temperature 20°C. Refrigerated water is added to it slowly. when the temperature of the glass reaches 10°C, small droplets condense on the outer surface. Calculate the relative humidity in the room. The boiling point of water at a pressure of 17.5 mm of mercury is 20°C and at 8.9 mm of mercury it is 10°C.
If a = 0.72 and r = 0.24, then the value of tr is ______.
Answer in brief:
A gas in a cylinder is at pressure P. If the masses of all the molecules are made one-third of their original value and their speeds are doubled, then find the resultant pressure.
Answer in brief:
Compare the rms speed of hydrogen molecules at 127ºC with rms speed of oxygen molecules at 27ºC given that molecular masses of hydrogen and oxygen are 2 and 32 respectively.
Find the kinetic energy of 5 litres of a gas at STP, given the standard pressure is 1.013 × 105 N/m2.
The emissive power of a sphere of area 0.02 m2 is 0.5 kcal s-1m-2. What is the amount of heat radiated by the spherical surface in 20 seconds?
If the density of nitrogen is 1.25 kg/m3 at a pressure of 105 Pa, find the root mean square velocity of nitrogen molecules.
The average translational kinetic energy of gas molecules depends on ____________.
Assuming the expression for the pressure exerted by the gas on the wall of the container, it can be shown that pressure is ______.
An ideal gas in a container of volume 500 cc is at a pressure of 2 × 105 N/m2. The average kinetic energy of each molecule is 6 × 10−21 J. The number of gas molecules in the container is ______.
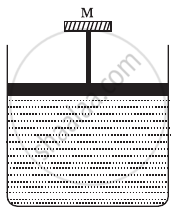
A cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (Figure). If the temperature is increased ______.
Two molecules of a gas have speeds of 9 × 10 6 ms−1 and 1 × 106 ms−1, respectively. What is the root mean square speed of these molecules?
Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. Assume the velocity is along x-axis and the area of cross-section of the block perpendicular to v0 is A. Show that the drag force on the block is `4ρAv_0 sqrt((KT)/m)`, where m is the mass of the gas molecule.
A proton, a deuteron and an α-particle with same kinetic energy enter into a uniform magnetic field at right angle to magnetic field. The ratio of the radii of their respective circular paths is ______.
When the temperature of an ideal gas is increased from 27°C to 227°C, its speed is changed from 400 ms-1 to vs, and Then vs is ______.
If a = 0. 72 and r = 0.24, then the value of t is ______.
Which of the following materials is diathermanous?
Show that the average energy per molecule is proportional to the absolute temperature T of the gas.
