Advertisements
Advertisements
Question
Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. Assume the velocity is along x-axis and the area of cross-section of the block perpendicular to v0 is A. Show that the drag force on the block is `4ρAv_0 sqrt((KT)/m)`, where m is the mass of the gas molecule.
Solution
Consider the diagram
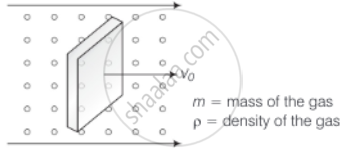
Let n = number of molecules per unit volume
Vrms = rms speed of the gas molecules
When a block is moving with speed v0, relative speed of molecules w.r.t. front face = v + v0
Coming head-on, momentum transferred to block per collision = 2m (v + v0), where, m = mass of the molecule.
The number of collisions in time Δt = m(v + v0)2nAΔt, where, A = area of cross-section of block and factor of 1/2 appears due to particles moving towards the block.
∴ The momentum transferred in time Δt = m(v + v0)2nAΔt from the front surface.
Similarly, momentum transferred in time Δt = m(v – v0)2nAΔt ......(From the back surface)
∴ Net force (drag force) = mnA[(v + v0)2 – (v – v0)2] .....[From front]
= mnA (4vv0)
= (4 mnAv)v0
= (4ρAv)v0 ......(i)
Where we have assumed ρ = `(mn)/V = M/V`
If v = velocity along the x-axis
Then, we can write KE = `1/2 mv^2 = 1/2 K_BT`
⇒ `v = sqrt((K_BT)/m)` .....`[(K_B = "Boltzmann constant"),(KE = "Kinetic energy"),(T = "Temperature")]`
∴ From equation (i), Drag force = (4ρAv)v0 = `4ρA sqrt((K_BT)/m) v_0`.
APPEARS IN
RELATED QUESTIONS
At what temperature the mean speed of the molecules of hydrogen gas equals the escape speed from the earth?
Use R = 8.314 JK-1 mol-1
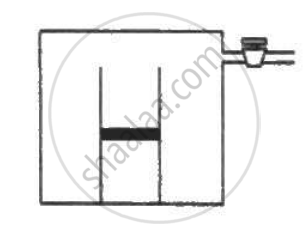
An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg in figure. The vessel itself is kept in a big chamber containing air at atmospheric pressure 100 kPa. The length of the gas column is 20 cm. If the chamber is now completely evacuated by an exhaust pump, what will be the length of the gas column? Assume the temperature to remain constant throughout the process.
At what temperature will oxygen molecules have same rms speed as helium molecules at S.T.P.? (Molecular masses of oxygen and helium are 32 and 4 respectively).
Answer in brief:
Compare the rms speed of hydrogen molecules at 127ºC with rms speed of oxygen molecules at 27ºC given that molecular masses of hydrogen and oxygen are 2 and 32 respectively.
Calculate the average molecular kinetic energy
- per kmol
- per kg
- per molecule
of oxygen at 127°C, given that the molecular weight of oxygen is 32, R is 8.31 J mol−1K−1 and Avogadro’s number NA is 6.02 × 1023 molecules mol−1.
The number of degrees of freedom, for the vibrational motion of a polyatomic molecule, depends on the ______
The average K.E. of hydrogen molecules at 27° C is E. The average K.E. at 627° C is ____________.
A molecule consists of two atoms each of mass 'm' and separated by a distance 'd'. At room temperature the average rotational kinetic energy is 'E', then its angular frequency is ______.
A cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (Figure). If the temperature is increased ______.
Which of the following materials is diathermanous?
