Advertisements
Advertisements
प्रश्न
Answer in brief:
Show that rms velocity of an oxygen molecule is `sqrt2` times that of a sulfur dioxide molecule at S.T.P.
उत्तर
`("M"_0 ("SO"_2))/("M"_0 ("O"_2)) = (64 "kg/mol")/(32 "kg/mol") = 2`
The rms speed, `"v"_"rms" = sqrt("3RT"/"M"_0)`
∴ `"v"_"rms" ∝ 1/sqrt"M"_0` at constant T
∴ `("v"_"rms"("O"_2))/("v"_"rms"("SO"_2)) = sqrt(("M"_0 ("SO"_2))/("M"_0 ("O"_2))) = sqrt2`
Thus, `"v"_"rms"("O"_2) = sqrt2 "v"_"rms"("SO"_2)`
APPEARS IN
संबंधित प्रश्न
Do you expect the gas in a cooking gas cylinder to obey the ideal gas equation?
It is said that the assumptions of kinetic theory are good for gases having low densities. Suppose a container is so evacuated that only one molecule is left in it. Which of the assumptions of kinetic theory will not be valid for such a situation? Can we assign a temperature to this gas?
If the molecules were not allowed to collide among themselves, would you expect more evaporation or less evaporation?
The mean square speed of the molecules of a gas at absolute temperature T is proportional to
The temperature and pressure at Simla are 15.0°C and 72.0 cm of mercury and at Kalka these are 35.0°C and 76.0 cm of mercury. Find the ratio of air density at Kalka to the air density at Simla.
Use R=8.314J K-1 mol-1
The average translational kinetic energy of air molecules is 0.040 eV (1 eV = 1.6 × 10−19J). Calculate the temperature of the air. Boltzmann constant k = 1.38 × 10−23 J K−1.
Air is pumped into the tubes of a cycle rickshaw at a pressure of 2 atm. The volume of each tube at this pressure is 0.002 m3. One of the tubes gets punctured and the volume of the tube reduces to 0.0005 m3. How many moles of air have leaked out? Assume that the temperature remains constant at 300 K and that the air behaves as an ideal gas.
Use R = 8.3 J K-1 mol-1
0.040 g of He is kept in a closed container initially at 100.0°C. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by 12 J.
Use R = 8.3 J K-1 mol-1
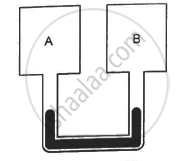
Figure shows two vessels A and B with rigid walls containing ideal gases. The pressure, temperature and the volume are pA, TA, V in the vessel A and pB, TB, V in the vessel B. The vessels are now connected through a small tube. Show that the pressure p and the temperature T satisfy `Ρ/T = 1/2 ({P_A}/{T_A}+{P_B}/{T_B))` when equilibrium is achieved.

An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg in figure. The vessel itself is kept in a big chamber containing air at atmospheric pressure 100 kPa. The length of the gas column is 20 cm. If the chamber is now completely evacuated by an exhaust pump, what will be the length of the gas column? Assume the temperature to remain constant throughout the process.
Figure shows two rigid vessels A and B, each of volume 200 cm3, containing an ideal gas (Cv = 12.5 J K−1 mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K. (a) Find the number of moles of the gas in each vessel. (b) 5.0 J of heat is supplied to the gas in vessel A and 10 J to the gas in vessel B. Assuming there's no appreciable transfer of heat from A to B, calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant, R = 8.3 J K−1 mol−1.
A glass contains some water at room temperature 20°C. Refrigerated water is added to it slowly. when the temperature of the glass reaches 10°C, small droplets condense on the outer surface. Calculate the relative humidity in the room. The boiling point of water at a pressure of 17.5 mm of mercury is 20°C and at 8.9 mm of mercury it is 10°C.
An adiabatic cylindrical tube of cross-sectional area 1 cm2 is closed at one end and fitted with a piston at the other end. The tube contains 0.03 g of an ideal gas. At 1 atm pressure and at the temperature of the surrounding, the length of the gas column is 40 cm. The piston is suddenly pulled out to double the length of the column. The pressure of the gas falls to 0.355 atm. Find the speed of sound in the gas at atmospheric temperature.
Calculate the average molecular kinetic energy
- per kmol
- per kg
- per molecule
of oxygen at 127°C, given that the molecular weight of oxygen is 32, R is 8.31 J mol−1K−1 and Avogadro’s number NA is 6.02 × 1023 molecules mol−1.
Compare the rates of emission of heat by a blackbody maintained at 727°C and at 227°C, if the black bodies are surrounded by an enclosure (black) at 27°C. What would be the ratio of their rates of loss of heat?
Under which condition laws of Boyle, Charles, and Gay-Lussac are valid?
On what, the values of absorption coefficient, reflection coefficient, and transmission coefficient depend, in addition to the material of the object on which the radiation is an incident?
Above what temperature, all bodies radiate electromagnetic radiation?
Compare the rate of radiation of metal bodies at 727 °C and 227 °C.
A metal cube of length 4 cm radiates heat at the rate of 10 J/s. Find its emissive power at a given temperature.
The average translational kinetic energy of gas molecules depends on ____________.
What is the microscopic origin of temperature?
Explain in detail the kinetic interpretation of temperature.
The average translational kinetic energy of a molecule in a gas is 'E1'. The kinetic energy of the electron (e) accelerated from rest through p.d. 'V' volt is 'E2'. The temperature at which E1 = E2 is possible, is ______.
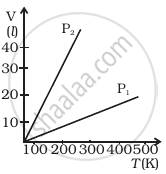
Volume versus temperature graphs for a given mass of an ideal gas are shown in figure at two different values of constant pressure. What can be inferred about relation between P1 and P2?
An insulated container containing monoatomic gas of molar mass m is moving with a velocity vo. If the container is suddenly stopped, find the change in temperature.
Assuming the expression for the pressure P exerted by an ideal gas, prove that the kinetic energy per unit volume of the gas is `3/2` P.
