Advertisements
Advertisements
प्रश्न
0.040 g of He is kept in a closed container initially at 100.0°C. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by 12 J.
Use R = 8.3 J K-1 mol-1
उत्तर
Here ,
m = 0.040g
M = 4g
n = \[\frac{0.040}{4} = 0.01 \]
T1 = (100 + 273) K = 373 K
He is a monoatomic gas. Thus,
\[\ C_v = 3 × (\frac{1}{2}R) \]
⇒ Cv = 1.5 × 8.3 = 12.45
Let the initial internal energy be U1 .
Let the final internal energy be U2 .
U2 -U1 = n Cv ( T2 -T1 )
⇒ 0.01 × 12.45( T2 - 373) = 12
⇒ T2 = 469 K
The temperature in °C can be obtained as follows: 469 - 273 = 196° C
APPEARS IN
संबंधित प्रश्न
Which of the following parameters is the same for molecules of all gases at a given temperature?
The process on an ideal gas, shown in figure, is
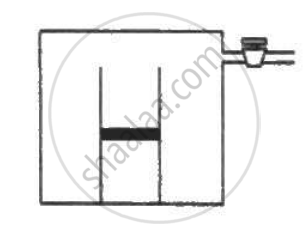
Figure shows two vessels A and B with rigid walls containing ideal gases. The pressure, temperature and the volume are pA, TA, V in the vessel A and pB, TB, V in the vessel B. The vessels are now connected through a small tube. Show that the pressure p and the temperature T satisfy `Ρ/T = 1/2 ({P_A}/{T_A}+{P_B}/{T_B))` when equilibrium is achieved.

One mole of an ideal gas undergoes a process `P = (P_0)/(1+(V/V_0)^2` where `p_0` and `V_0` are constants . Find the temperature of the gas when `V=V_0` .
An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg in figure. The vessel itself is kept in a big chamber containing air at atmospheric pressure 100 kPa. The length of the gas column is 20 cm. If the chamber is now completely evacuated by an exhaust pump, what will be the length of the gas column? Assume the temperature to remain constant throughout the process.
If a = 0.72 and r = 0.24, then the value of tr is ______.
Answer in brief:
Compare the rms speed of hydrogen molecules at 127ºC with rms speed of oxygen molecules at 27ºC given that molecular masses of hydrogen and oxygen are 2 and 32 respectively.
Compare the rates of emission of heat by a blackbody maintained at 727°C and at 227°C, if the black bodies are surrounded by an enclosure (black) at 27°C. What would be the ratio of their rates of loss of heat?
The number of degrees of freedom, for the vibrational motion of a polyatomic molecule, depends on the ______
Calculate the value of λmax for radiation from a body having a surface temperature of 3000 K. (b = 2.897 x 10-3 m K)
A metal cube of length 4 cm radiates heat at the rate of 10 J/s. Find its emissive power at a given temperature.
What is the microscopic origin of temperature?
The average translational kinetic energy of a molecule in a gas becomes equal to 0.49 eV at a temperature about (Boltzmann constant = 1.38 x 10-23 JK-1) ____________.
A molecule consists of two atoms each of mass 'm' and separated by a distance 'd'. At room temperature the average rotational kinetic energy is 'E', then its angular frequency is ______.
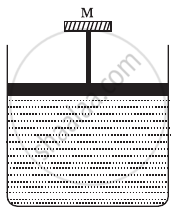
A cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (Figure). If the temperature is increased ______.
23Ne decays to 23Na by negative beta emission. Mass of 23Ne is 22.994465 amu mass of 23Na is 22.989768 amu. The maximum kinetic energy of emitted electrons neglecting the kinetic energy of recoiling product nucleus is ______ MeV.
A proton, a deuteron and an α-particle with same kinetic energy enter into a uniform magnetic field at right angle to magnetic field. The ratio of the radii of their respective circular paths is ______.
If a = 0. 72 and r = 0.24, then the value of t is ______.
