Advertisements
Advertisements
प्रश्न
Answer in brief:
Compare the rms speed of hydrogen molecules at 127ºC with rms speed of oxygen molecules at 27ºC given that molecular masses of hydrogen and oxygen are 2 and 32 respectively.
उत्तर
Data: M01 (hydrogen) = 2 g/mol,
M02 (oxygen) = 32 g/mol,
T1 (hydrogen) = 273 + 127 = 400 K,
T2 (oxygen) = 273 + 27 = 300 K
The rms speed, `"v"_"rms" = sqrt("3RT"/"M"_0)`,
where M0 denotes the molar mass
`therefore ("v"_"rms1" ("hydrogen"))/("v"_"rms2"("oxygen")) = sqrt(("T"_1/"T"_2)("M"_02/"M"_01))`
`= sqrt((400/300)(32/2)) = sqrt((4/3)(16))`
`= ((2)(4))/sqrt3 = 8/sqrt3`
APPEARS IN
संबंधित प्रश्न
It is said that the assumptions of kinetic theory are good for gases having low densities. Suppose a container is so evacuated that only one molecule is left in it. Which of the assumptions of kinetic theory will not be valid for such a situation? Can we assign a temperature to this gas?
When you come out of a river after a dip, you feel cold. Explain.
Find the number of molecules of an ideal gas in a volume of 1.000 cm3 at STP.
A gas cylinder has walls that can bear a maximum pressure of 1.0 × 106 Pa. It contains a gas at 8.0 × 105 Pa and 300 K. The cylinder is steadily heated. Neglecting any change in the volume, calculate the temperature at which the cylinder will break.
The average translational kinetic energy of air molecules is 0.040 eV (1 eV = 1.6 × 10−19J). Calculate the temperature of the air. Boltzmann constant k = 1.38 × 10−23 J K−1.
The mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.
Use R = 8.314 JK-1 mol-1
During an experiment, an ideal gas is found to obey an additional law pV2 = constant. The gas is initially at a temperature T and volume V. Find the temperature when it expands to a volume 2V.
Use R = 8.3 J K-1 mol-1
An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
The weather report reads, "Temperature 20°C : Relative humidity 100%". What is the dew point?
Figure shows two rigid vessels A and B, each of volume 200 cm3, containing an ideal gas (Cv = 12.5 J K−1 mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K. (a) Find the number of moles of the gas in each vessel. (b) 5.0 J of heat is supplied to the gas in vessel A and 10 J to the gas in vessel B. Assuming there's no appreciable transfer of heat from A to B, calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant, R = 8.3 J K−1 mol−1.
Using figure, find the boiling point of methyl alcohol at 1 atm (760 mm of mercury) and at 0.5 atm.

Answer in brief:
What will happen to the mean square speed of the molecules of a gas if the temperature of the gas increases?
Answer in brief:
A gas in a cylinder is at pressure P. If the masses of all the molecules are made one-third of their original value and their speeds are doubled, then find the resultant pressure.
Two vessels A and B are filled with the same gas where the volume, temperature, and pressure in vessel A is twice the volume, temperature, and pressure in vessel B. Calculate the ratio of the number of molecules of the gas in vessel A to that in vessel B.
Find the kinetic energy of 5 litres of a gas at STP, given the standard pressure is 1.013 × 105 N/m2.
Energy is emitted from a hole in an electric furnace at the rate of 20 W when the temperature of the furnace is 727°C. What is the area of the hole? (Take Stefan’s constant σ to be 5.7 × 10-8 Js-1 m-2K-4.)
Under which condition laws of Boyle, Charles, and Gay-Lussac are valid?
Above what temperature, all bodies radiate electromagnetic radiation?
Compare the rate of radiation of metal bodies at 727 °C and 227 °C.
A metal cube of length 4 cm radiates heat at the rate of 10 J/s. Find its emissive power at a given temperature.
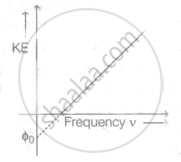
The graph of kinetic energy against the frequency v of incident light is as shown in the figure. The slope of the graph and intercept on X-axis respectively are ______.
When photons of energy hv fall on a metal plate of work function 'W0', photoelectrons of maximum kinetic energy 'K' are ejected. If the frequency of the radiation is doubled, the maximum kinetic energy of the ejected photoelectrons will be ______.
Assuming the expression for the pressure exerted by the gas on the wall of the container, it can be shown that pressure is ______.
The molecules of a given mass of a gas have root mean square speeds of 100 ms−1 at 27°C and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and 2.0 atmospheric pressure?
When a particle oscillates simple harmonically, its kinetic energy varies periodically. If frequency of the particle is n, then the frequency of the kinetic energy is ______.
If a = 0. 72 and t = 0.04, then the value of r is ______.
2000 calories of radiant heat is incident on a body. If the body absorbs 550 calories of heat, find the coefficient of emmission of the body.
